题目内容
【题目】如图所示，光滑水平面上有三个滑块A、B、C，质量分别为mA=2m，mB=m，mC=3m，A、B用细绳连接，中间有一压缩的轻弹簧（与滑块不栓接）． 开始时A、B以共同速度v0向右运动，C静止． 某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同．求：
①B、C碰撞前的瞬间B的速度；
②整个运动过程中，弹簧释放的弹性势能与系统损失的机械能之比．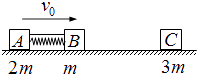
【答案】解：（i）A、B被弹开过程A、B系统动量守恒，以向右为正方向，由动量守恒定律得：
（mA+mB）v0=mAvA+mBvB，
对BC碰撞过程，由动量守恒定律得：（mC+mB）vC=mBvB，
且vC=vA，
解得：vC=vA=0.5v0，vB=2v0；
（ii）从绳剪断到AB与弹簧分开的过程，对AB和弹簧满足能量守恒，则有：
（m+2m）v 
+Ep= （2m）v 
+ mv 
解得：Ep= 
mv
根据全过程系统损失的机械能等于B、C碰撞前后损失的动能，则有：
△E损= mv ﹣ （m+3m）v 
解得：△E损= 
mv
则 
=
答：（i）B、C碰撞前的瞬间B的速度为2v0；
（ii）整个运动过程中，弹簧释放的弹性势能与系统损失的机械能之比为1：2
【解析】（1）弹簧弹开的过程满足动量守恒,B和C碰撞的过程也满足动量守恒根据动量守恒列式求解。
（2）从绳子剪断到两物体分离的过程，满足能量守恒能量守恒定律列式求解。
【考点精析】关于本题考查的动量守恒定律和能量守恒定律，需要了解动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变；能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移过程中，能量的总量保持不变才能得出正确答案．
