题目内容
(10分)如图所示,一高度为h="0." 2 m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0="5" m / s的速度在平面上向右运动,求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g="10" m / s2)。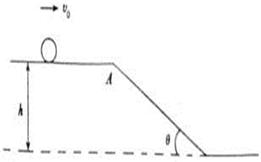

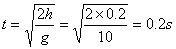
由于小球开始在水平面上运动,离开A点时小球将做平抛运动,而不会沿斜面下滑,在运动到地面之前小球是否经历斜面,要看以下条件:小球平抛到地面的水平距离为
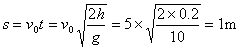 (3分)
(3分)
斜面底宽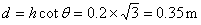 (2分)
(2分)
因为s>d,所以小球离开A点后不会落到斜面上。(2分)
因此落地时间即为平抛运动所需的时间。即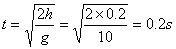 。(3分)
。(3分)
本题考查自由落体运动规律的应用,由竖直方向自由落体运动可求得运动时间,由水平方向匀速直线运动可求得水平位移大小,与斜面水平距离比较判断可知小球不会落在斜面上
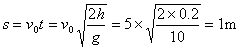 (3分)
(3分)斜面底宽
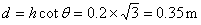 (2分)
(2分)因为s>d,所以小球离开A点后不会落到斜面上。(2分)
因此落地时间即为平抛运动所需的时间。即
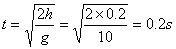 。(3分)
。(3分)本题考查自由落体运动规律的应用,由竖直方向自由落体运动可求得运动时间,由水平方向匀速直线运动可求得水平位移大小,与斜面水平距离比较判断可知小球不会落在斜面上

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目