题目内容
 如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.
如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.
解:设最大速度为v.从乙起跑到接棒的过程中,甲乙运动时间t相同.
对于乙,其运动为匀加速直线运动.设加速度为a,则:
a=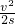 其中:s=25 m
其中:s=25 m
设乙从起跑到接棒奔跑的距离为s1,则:s1=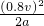 =16 m
=16 m
对于甲,其运动为匀速直线运动.设其在乙从起跑的接棒这段时间t内的位移为s2,则:t= 或t=
或t=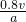
故:s2=vt=40 m
所以,乙起跑时,离甲的距离为:△s=s2-s1=24 m.
答:乙应在距甲24m处开始起跑.
分析:本题为追及相遇问题,注意要把握好其两个问题:时间和位移; 一个条件:速度相等; 根据位移相同及时间相等可列出关系式求解.
点评:解决追及相遇问题要分析两物体间的相互关系,再分别对两个物体列出位移时间关系,联立一定可解.
对于乙,其运动为匀加速直线运动.设加速度为a,则:
a=
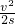 其中:s=25 m
其中:s=25 m设乙从起跑到接棒奔跑的距离为s1,则:s1=
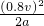 =16 m
=16 m对于甲,其运动为匀速直线运动.设其在乙从起跑的接棒这段时间t内的位移为s2,则:t=
 或t=
或t=
故:s2=vt=40 m
所以,乙起跑时,离甲的距离为:△s=s2-s1=24 m.
答:乙应在距甲24m处开始起跑.
分析:本题为追及相遇问题,注意要把握好其两个问题:时间和位移; 一个条件:速度相等; 根据位移相同及时间相等可列出关系式求解.
点评:解决追及相遇问题要分析两物体间的相互关系,再分别对两个物体列出位移时间关系,联立一定可解.

练习册系列答案
相关题目
 如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.
如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.