Question

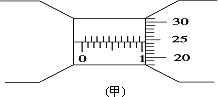
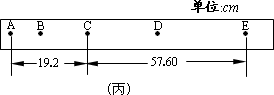
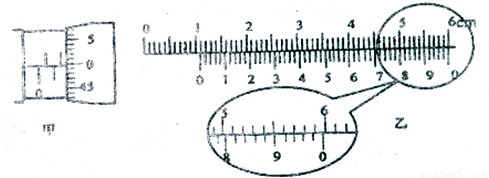
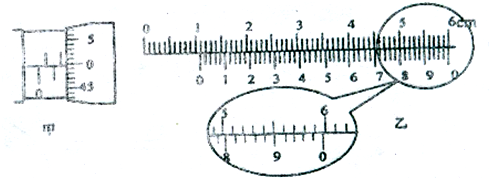
（1）图甲中螺旋测微器读数为______mm．图乙中游标卡尺读数为______cm．

（2）如图1所示，小车放在斜面上，车前段拴有不可伸长的细线，跨过固定在泄密那边缘的小滑轮与重物相连，小车后面与打点计时器的纸带相连接（已知细线与斜面平行）．起初小车停在靠近打点计时器的位置，重物到地面的距离小于小车道滑轮的距离．启动打点计时器，释放重物，小车在重物的牵引下，由静止开始沿斜面向上运动，重物落地后，小车会继续向上运动一段距离．打点计时器使用的交流电频率为50Hz．图2中a、b、c是小车运动纸带上的三段，纸带运动方向如箭头所示．
①根据所提供纸带上的数据，计算打c段纸带时小车的加速度大小为______m/s²．（结果保留两位有效数字）
②打a段纸带时，小车的加速度是2.5m/s²，请根据加速度的情况，判断小车运动的最大速度可能出现在b段纸带中对应长度为______的区域．
③如果 取g=10m/s²，由纸带数据可推断出重物与小车的质量比为______．

Answer 1

解：（1）螺旋测微器的固定刻度为1.5mm，可动刻度为49.7×0.01mm=0.497mm，所以最终读数为1.5mm+0.497mm=1.997mm．
游标卡尺的主尺读数为：1cm=10mm，游标尺上第47个刻度和主尺上某一刻度对齐，所以游标读数为47×0.02mm=0.94mm，所以最终读数为：10mm+0.94mm=10.94mm=1.094cm．
（2）①C段的加速度为了减小误差，采用逐差法
a_C==-5.0m/s²
②b段中只有2.98的位移最大，所以最大速度一定在2.98的区域．
③c段时，a_C=-5m/s²，设：斜面的夹角为θ，Mgsinθ=Ma_C sinθ=
A段时，a_a=2.5m/s²，mg-Mgsinθ=（m+M）a_a，解得：m：M=1：1．
故答案为：（1）1.997，1.094 （2）5.0 2.98 1：1
分析：打点计时器打点的时间间隔是相等的，观察纸带上相邻点间的距离的变化，判断纸带的运动情况．
根据匀变速直线运动的推论公式△x=aT²可以求出加速度的大小．
点评：解决实验问题首先要掌握该实验原理，了解实验的操作步骤和数据处理以及注意事项．其中平衡摩擦力的原因以及做法在实验中应当清楚．