题目内容
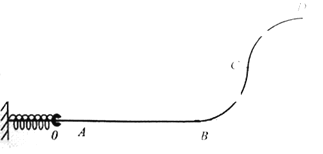
【题目】如图所示，将一根弹簧和一个小圆环穿在水平细杆上，弹簧左端固定，右端与质量为m的小圆环相接触，BC和CD是由细杆弯成的1/4圆弧，BC分别与杆AB和弧CD相切，两圆弧的半径均为R。O点为弹簧自由端的位置。整个轨道竖直放置，除OB段粗糙外，其余部分均光滑。当弹簧的压缩量为d时释放，小圆环弹出后恰好能到达C点，返回水平杆时刚好与弹簧接触，停在O点，（已知弹簧弹性势能与压缩量的平方成正比，小球通过B处和C处没有能量损失），问：
（1）当为弹簧的压缩量为d时，弹簧具有的弹性势能
是多少？
（2）若将小圆环放置在弹簧的压缩量为2d时释放，求小圆环到达最高点D时，轨道所受到的作用力。
（3）为了使物块能停在OB的中点，弹簧应具有多大的弹性势能？
【答案】（1）
（2）9mg，方向竖直向上（3）
（n=0、1、2）
【解析】
（1）设小圆环与OB之间的摩擦力为f，OB=L；从释放到回到O点，由能量关系可知，当弹簧的压缩量为d时，弹簧具有的弹性势能
小圆环从释放能到达C点到，由能量关系可知
可得：
（2）因弹簧弹性势能与压缩量的平方成正比，则弹簧的压缩量为2d时弹性势能为
EP=4EP=8mgR
小圆环到达最高点D时：
解得
在最高点D时由牛顿第二定律：
解得
N=9mg，方向竖直向下
由牛顿第三定律可知在D点时轨道受到的作用为9mg，方向竖直向上；
（3）为了使物块能停在OB的中点，则要求滑块到达的最高点为D点，然后返回，则
为了使物块能停在OB的中点，同时还应该满足：
则只能取n=0、1、2；
练习册系列答案
相关题目
