题目内容
12.某打捞船在河边发现观察点下游河中心有可疑物品顺流而下,船和物品的连线与下游河岸的夹角为60°时,船头立即对准物品前往打捞.设河宽为d,各处水流速度与船对静水的速度大小均为v,则打捞船追上物品的过程中,航行时间和航程分别为( )| A. | $\frac{\sqrt{3}d}{3v}$;d | B. | $\frac{\sqrt{3}d}{3v}$;$\frac{\sqrt{3}d}{2}$ | C. | $\frac{d}{2v}$;$\frac{\sqrt{3}d}{2}$ | D. | $\frac{d}{2v}$;d |
分析 将船的运动分解为垂直于河岸方向和沿河岸方向,抓住分运动与合运动具有等时性求出船运动的时间以及位移.
解答 解:由题可知,船头与下游河岸之间的夹角是60°,所以船垂直于河岸的分速度:
vy=v•sin60°=$\frac{\sqrt{3}}{2}$v
船沿河岸相对于水的分速度:
vx=v•cos60°=0.5v
所以船沿河岸的方向相对于河岸的分速度:
vx′=vx+v=1.5v
由于船头正对可疑物品运动,所以船运动到河的中央时,恰好追上可疑物品,所以运动的时间:
t=$\frac{\frac{d}{2}}{{v}_{y}}$=$\frac{\frac{d}{2}}{\frac{\sqrt{3}v}{2}}$=$\frac{\sqrt{3}d}{3v}$
船沿河岸方向的位移:
x=vx′•t=1.5v×$\frac{\sqrt{3}d}{3v}$=$\frac{\sqrt{3}}{2}$d
船的总位移:s=$\sqrt{{x}^{2}+(\frac{d}{2})^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2}d)^{2}+(\frac{d}{2})^{2}}$=d
故选:A.
点评 解决本题的关键知道分运动与合运动具有等时性,各分运动具有独立性,互不干扰,注意列出方程组,从而求解是解题的基本思路.

练习册系列答案
相关题目
2.关于参考系,下列说法正确的是( )
| A. | 当研究物体的运动时,应先确定参考系 | |
| B. | 描述一个物体的运动时,参考系可以任意选取 | |
| C. | 参考系必须选取地面或相对于地面静止不动的物体 | |
| D. | 研究地面上的物体的运动时只能选取地面为参考系 |
3.电场强度E的定义式为E=$\frac{F}{q}$,下列说法错误的是( )
| A. | 这个定义适用于任何电场 | |
| B. | 上式中F是放入电场中的电荷所受的力,q是放入电场中的电荷的电荷量 | |
| C. | 上式中F是放入电场中的电荷所受的力,q是产生电场的电荷的电荷量 | |
| D. | 在库仑定律的表达式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$中,k$\frac{{q}_{2}}{{r}^{2}}$是点电荷q2产生的电场在点电荷q1处的场强大小;而k$\frac{{q}_{1}}{{r}^{2}}$是点电荷q1产生的电场在点电荷q2处的场强大小 |
7. A和B两个物体同时由同一地点向同一方向做直线运动,它们的v-t图线如图所示,则下面叙述正确的是( )
A和B两个物体同时由同一地点向同一方向做直线运动,它们的v-t图线如图所示,则下面叙述正确的是( )
 A和B两个物体同时由同一地点向同一方向做直线运动,它们的v-t图线如图所示,则下面叙述正确的是( )
A和B两个物体同时由同一地点向同一方向做直线运动,它们的v-t图线如图所示,则下面叙述正确的是( )| A. | t2时刻之前A的速度比B的大 | |
| B. | 0~t1这段时间内A的速度变化比B快 | |
| C. | 两物体在t2时刻相遇 | |
| D. | t2时刻之前A在B的前面,且AB之间的距离在增大 |
4.下列物理公式属于定义式的是( )
| A. | P=Fv | B. | a=$\frac{F}{m}$ | C. | ω=$\frac{υ}{r}$ | D. | E=$\frac{F}{q}$ |
1.利用打点计时器测定物体做匀变速直线运动的加速度时,在纸带上打出一系列的点(舍去前面过于密集的点),如图所示.设相邻计数点之间的距离分别为s1、s2…,相邻计数点的时间间隔为T,则下列关系中正确的是( )


| A. | s2-s1=aT2 | |
| B. | s4-s1=3aT2 | |
| C. | 与计数点2对应的速度为v2=$\frac{({s}_{2}+{s}_{1})}{2T}$ | |
| D. | s1=$\frac{1}{2}$aT2 |
2.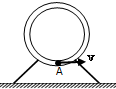 如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )
如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )
 如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )
如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )| A. | 小球恰能做完整的圆周运动 | |
| B. | 小球沿圆轨道上升的最大高度为0.4m | |
| C. | 圆管对底座的最大压力为15N | |
| D. | 圆管对底座的最大压力等于25N |