题目内容

从地面发射质量为m的导弹，导弹上的喷气发动机可产生恒定的推力，且可通过改变喷气发动机尾喷管的喷气质量和方向改变发动机推力的大小和方向，导弹起飞时发动机推力大小为F= $数学公式$ mg导弹沿和水平方向成θ=30°角的直线斜向上方匀加速飞行．经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原有向匀减速直线飞行．（不计空气阻力和喷气过程中导弹质量的变化）．求：
（1）t时刻导弹的速率及位移是多少？
（2）旋转方向后导弹还要经过多长时间到达最高点？

解：（1）开始阶段，导弹受到重力和推力，其合力沿和水平方向成θ=30°角的直线斜向右上方，如左图所示，由几何关系得：F_合=mg，则得加速度为a₁=g．
所以t时刻导弹的速率为：v=a₁t=gt
位移：x= $\text{[math]}$ = $\text{[math]}$
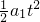（2）t时刻后，导弹的加速度方向与原速度v的方向相反，如右图所示，则加速度大小为：a₂= $\text{[math]}$ =0.5g
则有：v=a₂t′，又v=gt
所以得：t′=2t
即旋转方向后导弹还要经过2t时间到达最高点．
答：（1）t时刻导弹的速率为gt，位移是 $\text{[math]}$ ．
（2）旋转方向后导弹还要经过2t时间到达最高点．
分析：（1）导弹沿和水平方向成θ=30°角的直线斜向右上方匀加速飞行．其合力也沿此方向．导弹受到重力和推力，根据平行四边形定则作出合力，由几何知识求出合力，由牛顿第二定律求出导弹的加速度，由运动学公式求解t时刻导弹的速率及位移．
（2）经过时间t后，导弹沿原有向匀减速直线飞行，其合力与速度方向相反，由平行四边形定则作出合力，根据牛顿第二定律求出加速度，由运动学公式求出导弹到达最高点所用时间．
点评：本题的解题关键是根据物体直线运动的条件，确定出导弹的合力方向，由平行四边形定则求出合力．

练习册系列答案

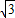mg导弹沿和水平方向成θ=30°角的直线斜向上方匀加速飞行．经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原有向匀减速直线飞行．（不计空气阻力和喷气过程中导弹质量的变化）．求：
（1）t时刻导弹的速率及位移是多少？
（2）旋转方向后导弹还要经过多长时间到达最高点？

mg，导弹沿和水平方向成θ=30°角的直线斜向右上方匀加速飞行．经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原方向匀减速直线飞行．（不计空气阻力和喷气过程中导弹质量的变化）．求
（1）t时刻导弹的速率及位移是多少？
（2）旋转方向后导弹还要经过多长时间到达最高点？
（3）导弹上升的最大高度是多少？

从地面发射质量为m的导弹，导弹上的喷气发动机可产生恒定的推力，且可通过改变喷气发动机尾喷管的喷气质量和方向改变发动机推力的大小和方向，导弹起飞时发动机推力大小为F＝mg，导弹沿和水平方向成θ＝30°角的直线斜向右上方匀加速飞行。经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原方向匀减速直线飞行。(不计空气阻力和喷气过程中导弹质量的变化)则：

(1)旋转方向后推力的大小为多少?

(2)旋转方向后导弹还要经过多长时间到达运动中的最高点?

(3)导弹上升到最高点时离出发点的距离是多少?

从地面发射质量为m的导弹，导弹上的喷气发动机可产生恒定的推力，且可通过改变喷气发动机尾喷管的喷气质量和方向改变发动机推力的大小和方向，导弹起飞时发动机推力大小为F＝mg，导弹沿和水平方向成θ＝30°角的直线斜向右上方匀加速飞行。经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原方向匀减速直线飞行。（不计空气阻力和喷气过程中导弹质量的变化）则：
（1）旋转方向后推力的大小为多少？
（2）旋转方向后导弹还要经过多长时间到达运动中的最高点？
（3）导弹上升到最高点时离出发点的距离是多少？

试题分类