题目内容
如图所示,竖直平面内固定轨道ABC,由水平粗糙轨道AB和四分之一光滑圆弧轨道BC组成,AB恰与圆弧BC在B点相切。质量m=1kg的小物块从A点以水平初速度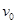 =6m/s滑上轨道AB,滑上圆弧轨道BC后返回。已知水平轨道AB长为L=5m,圆弧半径R=1m,小物块与AB轨道间的动摩擦因数为
=6m/s滑上轨道AB,滑上圆弧轨道BC后返回。已知水平轨道AB长为L=5m,圆弧半径R=1m,小物块与AB轨道间的动摩擦因数为 =0.2,取重力加速度g=10m/s2。求:
=0.2,取重力加速度g=10m/s2。求:

(1)小物块滑到B点时速度的大小;
(2)小物块在圆弧轨道B处对轨道压力的大小;
(3)通过计算说明小物块最终能否从A处脱离轨道。
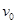 =6m/s滑上轨道AB,滑上圆弧轨道BC后返回。已知水平轨道AB长为L=5m,圆弧半径R=1m,小物块与AB轨道间的动摩擦因数为
=6m/s滑上轨道AB,滑上圆弧轨道BC后返回。已知水平轨道AB长为L=5m,圆弧半径R=1m,小物块与AB轨道间的动摩擦因数为 =0.2,取重力加速度g=10m/s2。求:
=0.2,取重力加速度g=10m/s2。求:
(1)小物块滑到B点时速度的大小;
(2)小物块在圆弧轨道B处对轨道压力的大小;
(3)通过计算说明小物块最终能否从A处脱离轨道。
(1) (2)
(2) (3)小物块不能从A处脱离轨道
(3)小物块不能从A处脱离轨道
 (2)
(2) (3)小物块不能从A处脱离轨道
(3)小物块不能从A处脱离轨道(1)A到B过程中由动能定理 (3分)
(3分)
得: (1分)
(1分)
(2)在B处对小物块进行受力分析,由牛顿第二定律 (3分)
(3分)
得: (1分)又由牛顿第三定律得
(1分)又由牛顿第三定律得 (1分)
(1分)
(3)设物块从B处向右运动的最大距离为 ,由动能定理
,由动能定理 (3分)
(3分)
得: 所以小物块不能从A处脱离轨道。(3分)
所以小物块不能从A处脱离轨道。(3分)
说明:用其他方法证明,如“比较能量关系”等,只要合理,也可给分。
本题考查动能定理和圆周运动规律,从A到B过程中,物块克服摩擦力做功,求得B点速度大小,B点为圆周运动的最低点,受力并不平衡,由合力提供向心力,可求得支持力大小
 (3分)
(3分)得:
 (1分)
(1分)(2)在B处对小物块进行受力分析,由牛顿第二定律
 (3分)
(3分)得:
 (1分)又由牛顿第三定律得
(1分)又由牛顿第三定律得 (1分)
(1分)(3)设物块从B处向右运动的最大距离为
 ,由动能定理
,由动能定理 (3分)
(3分)得:
 所以小物块不能从A处脱离轨道。(3分)
所以小物块不能从A处脱离轨道。(3分)说明:用其他方法证明,如“比较能量关系”等,只要合理,也可给分。
本题考查动能定理和圆周运动规律,从A到B过程中,物块克服摩擦力做功,求得B点速度大小,B点为圆周运动的最低点,受力并不平衡,由合力提供向心力,可求得支持力大小

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目





 mv
mv
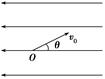
 ,如图所示,则小木块从放到传送带上开始到与传送带相对静止的过程中,转化为内能的能量为
,如图所示,则小木块从放到传送带上开始到与传送带相对静止的过程中,转化为内能的能量为



