Question

（1）有一只匀质椭球形玻璃球，长轴为8cm．短轴为4

3

cm，在椭球的焦点F处有一小气泡，为了测定该玻璃椭球的折射率，某同学将球的上半部表面涂黑，只在球顶A处留出一小块可以透光的地方，如图所示，从A处去看气泡，当视线与短轴的夹角为45⁰时，恰好看到气泡，则该玻璃的折射率为

B

 　A.4/3   　 B．

2

    　C.2   　  D．

6

（2）在均匀介质中选取平衡位置在同一直线上的9个质点，相邻两质点间的距离均为0.1m，如图（a）所示．一列横波沿该直线向右传播，t=0时到达质点1，质点1开始向下运动，振幅为0.2m，经过时间0.3s第一次出现如图（b）所示的波形．  ①求该列横波传播的速   ②写出质点1的振动方程．

Answer 1

分析：（1）先根据数学知识求出焦点F的坐标，光线从F出发，射到A点，经折射进入该同学的眼中，由几何知识求出入射角i，由折射定律求出的折射率．
（2）①质点1开始向下运动，而图b中质点1的运动方向向上，说明第一次出现如图（b）所示的波形经过了1.5T．求出时间，读出波长，再求出波速．②质点起振方向向下，由振幅和周期，可写出振动方程．

解答：解：（1）作出光路图如图所示，焦点F的坐标为c=

a2-b2

=

82-(4 3 )2

cm=4cm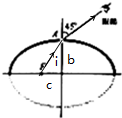
设入射角为i，则tani=

c

b

=

4

4 3

=

3

3

，得i=30°
折射角r=45°
故折射率为n=

sinr

sini

=

2

（2）①根据题意，质点1开始向下运动，而图b中质点1的运动方向向上，说明第一次出现如图（b）所示的波形经过了1.5T．即有t=0.3s=1.5T，得到周期为T=0.2s
从图中可以看出，波长λ=0.8 m，根据波速公式得到，波速为v=

λ

T

=

0.8

0.2

m/s=4m/s
②质点1开始从平衡位置向下运动，振幅为A=0.2m，则质点1的振动方程为y=-Asin

2π

T

t=-0.2sin（10πt）m
故答案为：
（1）B；
（2）①4m/s；②x=-0.2sin（10πt）m

点评：第2题是关键是确定时间t=0.3s与周期的关系，容易产生的错误是认为t=0.2s=T，要抓住各质点起振方向都相同．