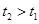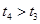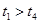题目内容
如图蜘蛛在地面于竖直墙壁间结网,蛛丝AB与水平地面之间的夹角为450,A到地面的距离为1m,已知重力加速度g取10m/s2,空气阻力不计,若蜘蛛从竖直墙上距地面0.8m的C点以水平速度v0跳出,要到达蛛丝,水平速度v0可以为 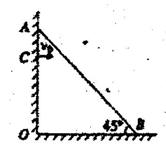
| A.1m/s | B.2m/s | C.3.5m/s | D.1.5m/s |
BC
解析试题分析:蜘蛛做平抛运动,设水平位移为x,竖直位移为y,则x=y+0.2m…① 
② ③,若蜘蛛到达网是恰好与网相切,应有:
③,若蜘蛛到达网是恰好与网相切,应有: ,联立得水平速度v0为2m/s,只要速度大于2m/s就可以到达网丝AB,所以BC正确,AD错误。
,联立得水平速度v0为2m/s,只要速度大于2m/s就可以到达网丝AB,所以BC正确,AD错误。
考点:本题考查了平抛运动的规律。

一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示.则此时小球水平速度与竖直速度之比、小球水平方向通过的距离与在竖直方向下落的距离之比分别为( )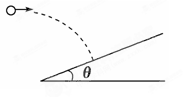
| A.水平速度与竖直速度之比为tanθ |
B.水平速度与竖直速度之比为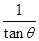 |
| C.水平位移与竖直位移之比为2tanθ |
D.水平位移与竖直位移之比为 |
如图所示,一网球运动员将球在边界处正上方正对球网水平向前击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法中正确的是 ( )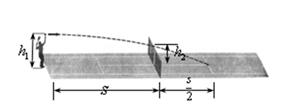
| A.击球点高度h1与球网高度h2之间的关系为h1 =1.8h2 |
B.若保持击球高度不变,球的初速度满足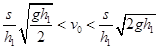 ,一定落在对方界内 ,一定落在对方界内 |
| C.任意降低击球高度(仍大于h2),只要击球初速度合适,球一定能落在对方界内 |
| D.任意增加击球高度,只要击球初速度合适,球一定能落在对方界内 |
如图所示,在竖直面内有一个圆轨道,圆心为O。P为轨道上与O等高的最右端位置,一小球以某一初速度从p点水平向左抛出,落在圆轨道上的某一点,忽略一切阻力和能量损耗,则下列说法正确的是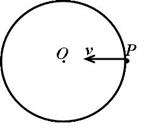
| A.小球初速度合适,可能垂直撞在圆轨道上 |
| B.小球初速度合适,位移大小等于直径 |
| C.初速度越大,落到圆轨道上的时间越长 |
| D.小球初速度合适,落在O点正下方的圆周上时间最长 |
如图所示,在一次空地演习中,离地H高处的飞机以水平速度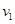 发射一颗炮弹欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度
发射一颗炮弹欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度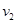 竖直向上发射炮弹拦截. 设拦截系统与飞机的水平距离为s,若拦截成功,不计空气阻力,则
竖直向上发射炮弹拦截. 设拦截系统与飞机的水平距离为s,若拦截成功,不计空气阻力,则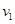 、
、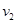 的关系应满足
的关系应满足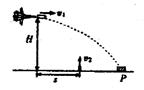
A.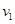 = =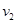 | B.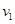 = =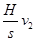 |
C.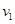 = =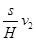 | D.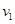 = =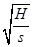 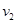 |
如图所示,放置在竖直平面内的光滑杆AB,是按照从高度为h处以初速度v0平抛的运动轨迹制成的,A端为抛出点,B端为落地点,现将一小球套于其上,由静止开始从轨道A端滑下,已知重力加速度为g,当小球到达轨道B端时( )
A.小球的速率为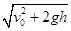 |
B.小球的速率为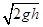 |
| C.小球在水平方向的速度大小为v0 |
D.小球在水平方向的速度大小为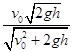 |
图中竖直平面xOy内存在有竖直向下的电场,带电小球以初速度v0从O点沿x轴水平射入,恰好通过平面中的A点,OA连线与Ox夹角为300,已知小球质量为m,则带电小球通过A点时的动能为( )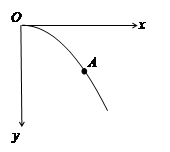
A.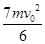 | B.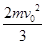 | C.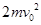 | D.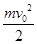 |
如图所示,小球从楼梯上以2m/s的速度水平抛出,所有台阶的高度和宽度均为0.25m,g取10/s2,小球抛出后首先落到的台阶是( )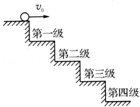
| A.第一级台阶 | B.第二级台阶 | C.第三级台阶 | D.第四级台阶 |
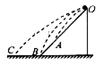
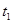 ,若给小球不同的水平初速度,落到斜面上的A点,经过的时间是
,若给小球不同的水平初速度,落到斜面上的A点,经过的时间是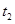 ,落到斜面底端B点,经过的时间是
,落到斜面底端B点,经过的时间是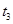 ,落到水平面上的C点,经过的时间是
,落到水平面上的C点,经过的时间是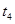 ,则( )
,则( )