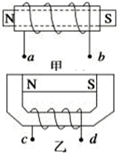
题目内容
(1)若金属线圈的电阻为R,求金属线圈的ab边刚进入区域1 的瞬间,线圈克服安培力做功的功率为多少?
(2)若金属线圈的质量为m ,求金属线圈通过区城l 的过程中,线圈中产生了多少热量?
(3)若金属线圈的质量和电阻均为未知,求线圈通过第二个磁场区域后(cd 边离开磁场)的速度。

(1)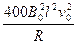 (2)
(2)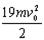 (3)8 v0
(3)8 v0
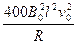 (2)
(2)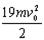 (3)8 v0
(3)8 v0(1)ab边刚进入时,线圈产生的感应电动势为
E =B0·2l·10v0 (2分)
线圈中电流为 I =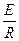 (2 分)
(2 分)
安培力为F = B0·I·2l (2 分)
克服安培力做功的功率为P =F·10 v0=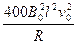 (2 分)
(2 分)
(2)由能量守恒,线圈中产生的焦耳热为
Q =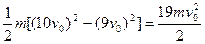 (4 分)
(4 分)
(3)设线圈与第一个磁场区域重合时的速度为v1,由动旦定理可得
—B0·2l· I1t 1= m v1— m·10 v0 ( 1 分)
—B0·2l· I2t 2= m·9v0— m v1 ( l 分)
q=I1t 1= I2t 2=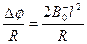 ( l 分)
( l 分)
解得: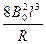 = m v0 ( 1 分)
= m v0 ( 1 分)
同理,线圈通过第二个区域时,由动量定理可得
—B0·2l· I3t 3= m v2—m·9v0 ( l 分)
—B0·2l· I4t 4= mv3— m v2 ( l 分)
q= I3t 3= I4t 4=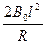
解得:v3=8 v0 ( l 分)
E =B0·2l·10v0 (2分)
线圈中电流为 I =
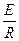 (2 分)
(2 分)安培力为F = B0·I·2l (2 分)
克服安培力做功的功率为P =F·10 v0=
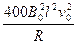 (2 分)
(2 分)(2)由能量守恒,线圈中产生的焦耳热为
Q =
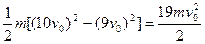 (4 分)
(4 分)(3)设线圈与第一个磁场区域重合时的速度为v1,由动旦定理可得
—B0·2l· I1t 1= m v1— m·10 v0 ( 1 分)
—B0·2l· I2t 2= m·9v0— m v1 ( l 分)
q=I1t 1= I2t 2=
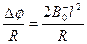 ( l 分)
( l 分)解得:
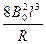 = m v0 ( 1 分)
= m v0 ( 1 分)同理,线圈通过第二个区域时,由动量定理可得
—B0·2l· I3t 3= m v2—m·9v0 ( l 分)
—B0·2l· I4t 4= mv3— m v2 ( l 分)
q= I3t 3= I4t 4=
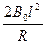
解得:v3=8 v0 ( l 分)

练习册系列答案
相关题目