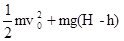题目内容
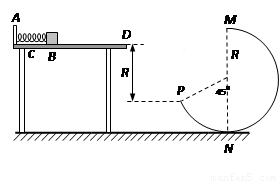
如图所示,水平桌面上有一轻弹簧,左端固定在A点,弹簧处于自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R="0.8" m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧也缓慢压缩到C点释放,物块过B点后其位移与时间的关系为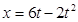 ,物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道。g ="10" m/s2,求:
,物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道。g ="10" m/s2,求:
(1)BP间的水平距离;
(2)判断m2能否沿圆轨道到达M点;
(3)释放后m2在水平桌面上运动过程中克服摩擦力做的功。
(1) 4.1m (2) 不能(3)
【解析】
试题分析:(1)设物块由D点以初速度 做平抛,落到P点时其竖直速度为vy ,有
做平抛,落到P点时其竖直速度为vy ,有
 而
而 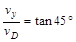 解得
解得  (2分)
(2分)
设平抛运动时间为t,水平位移为x1,有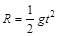
 解得
解得 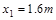 (2分)
(2分)
由题意可知小球过B点后做初速度为
BD间位移为x2 ,有 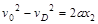
所以BP水平间距为  = 4.1m (2分)
= 4.1m (2分)
(2)若物块能沿轨道到达M点,其速度为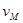 ,有
,有
 (2分)
(2分)
解得:  <
< 
即 物块不能到达M点 (2分)
(3)设弹簧长为AC时的弹性势能为EP,物块与桌面间的动摩擦因数为μ

释放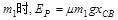
释放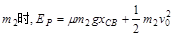
解得  J (3分)
J (3分)
设 在桌面上运动过程中克服摩擦力做功为Wf,有
在桌面上运动过程中克服摩擦力做功为Wf,有
 解得
解得  (2分)
(2分)
考点:考查了机械能守恒定律、平抛运动基本公式、圆周运动向心力公式的应用
点评:该题涉及到多个运动过程,主要考查了机械能守恒定律、平抛运动基本公式、圆周运动向心力公式的应用,用到的知识点及公式较多,难度较大,属于难题.

 千里马走向假期期末仿真试卷寒假系列答案
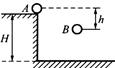
千里马走向假期期末仿真试卷寒假系列答案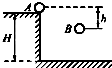 如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )A、
| ||||
B、
| ||||
| C、mgH-mgh | ||||
D、
|
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能的表达式正确的是( ) 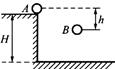
A. | B. |
| C.mgH-mgh | D. |


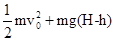

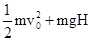 B.
B.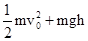


 B.
B.