题目内容
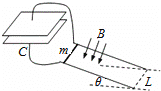
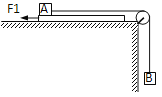
【题目】一个木板放置在光滑的水平桌面上,A、B两个小物体通过不可伸长的轻绳相连,并且跨过光滑的定滑轮,A物体(可视为质点)放置在木板的最左端,滑轮与物体A间的细绳平行于桌面.已知木板的质量m1=20kg,物体A的质量m2=4kg,物体B的质量m3=lkg,物体A与木板间的动摩擦因数μ=0.5,木板长L=2m,木板与物体A之间的最大静摩擦力等于滑动摩擦力.为了使A、B两个物体以及木板均保持静止状态,需要对木板施加水平向左的力F1.(重力加速度g取l0m/s2)
(1)求F1的大小;
(2)为了使物体A随着木板一起向左运动,并且不发生相对滑动,现把力F1替换为水平向左的力F2,求力F2的最大值;
(3)若对木板施加水平向左的力F3=80N,则物体A滑到木板的最右端所用时间为多少?
【答案】(1)10N;(2)60N;(3)2s;
【解析】(1)对物体B受力分析由平衡条件得:T1=m3g
对物体A和木板组成的整体受力分析,由平衡条件得:F1=T1
得:F1=10N
(2)运动过程中,三个物体的加速度大小相等,设加速度大小为α
对物体B受力分析,根据牛顿第二定律有:T2﹣m3g=m3α
对物体A受力分析,根据牛顿第二定律有:μm2g﹣T2=m2α
解得:α=2.0m/s2
对木板受力分析.根据牛顿第二定律有:F2﹣μm2g=m1α
解得F2=60N
(3)由题意知所加力F3大于F2木板与A发生相对滑动,对木板有:
F3﹣μm2g=m1α1
解得:α1=3m/s2
对A、B为整体有:μm2g﹣m3g=(m2+m3)α2
解得α2=2m/s2
又: ![]()
解得:t=2s

练习册系列答案
相关题目