题目内容
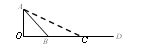
如图所示，DO是水平面，AB是斜面，物体由初速度为零开始从A点沿ABD滑到D点，到达D点时速度为V，如果斜面改为AC，则物体由初速度为零开始从A点沿ACD滑到D点时的速度为（已知物体与接触面之间的动摩擦因数处处相同且不为零，转折点B或C处有一小段圆弧与斜面和水平面相切可使物块平稳的滑到水平面，此段弧长可忽略）（ ）分析：物体从A点沿ABD滑动到D点的过程中，分为水平和斜面两个过程，由于只有重力和摩擦力做功，根据动能定理列式求解即可．
解答：解：物体从A点沿ABD滑动到D点的过程中，根据动能定理得
mg?hAO-μmg?xBD-μmgcosθ?xAB=
mv2
由几何关系cosθ?xAB=xOB，因而上式可以简化为
mg?hAO-μmg?xBD-μmg?xOB=
mv2，
即得到 mg?hAO-μmg?xOD=
mv2，
从上式可以看出，到达D点的动能与路径无关，故知物体沿AC滑到D点的速度为v．故C正确．
故选C
mg?hAO-μmg?xBD-μmgcosθ?xAB=
| 1 |
| 2 |
由几何关系cosθ?xAB=xOB，因而上式可以简化为
mg?hAO-μmg?xBD-μmg?xOB=
| 1 |
| 2 |
即得到 mg?hAO-μmg?xOD=
| 1 |
| 2 |
从上式可以看出，到达D点的动能与路径无关，故知物体沿AC滑到D点的速度为v．故C正确．
故选C
点评：本题关键根据动能定理列式，对列得的方程进行讨论得出结论．
练习册系列答案
相关题目
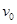的物体从D点出发沿DBA滑动到顶点A时速度刚好为零，如果斜面改为AC，让该物体从D点出发沿DCA滑动到A点且速度刚好为零。则物体具有的初速度（已知物体与路面之间的动摩擦因数处处相同且不为零）
（ ）
的物体从D点出发沿DBA滑动到顶点A时速度刚好为零，如果斜面改为AC，让该物体从D点出发沿DCA滑动到A点且速度刚好为零。则物体具有的初速度（已知物体与路面之间的动摩擦因数处处相同且不为零） （ ）