题目内容
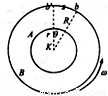
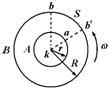1920年科学家斯特恩运用圆周运动规律测定了气体分子（银蒸汽分子）速度的大小．实验装置如图所示，A、B为半径分别为r、R的共轴圆柱形容器，它们可以相同的角速度绕同一轴高速旋转，其内部为真空．一根镀银的铂丝k沿几何轴安装，通电使其加热，银分子（即原子）蒸发形成气体．当圆柱筒静止时，银分子（原子）通过A筒上的狭缝a射到外筒壁上，在筒壁上形成一条附着线b；当圆柱筒以角速度ω逆时针高速转动时，附着线移至b′处，两附着线间的弧长为s，则分子的运动速率分析：气体分子做匀速直线运动，转盘做匀速圆周运动，两种运动同时发生，互不影响；气体分子从a到达b的过程中，转盘盘上外边缘点转过s的弧长，根据时间相等并结合v=ωR列式计算．
解答：解：气体分子运动和转盘转动同时发生，互不影响；这个实验运用了运动的等时性规律测定．
气体分子运动时间为：t=
转盘边缘上点线速度为，故转动时间为：t=
；
两个运动同时发生，故t=
=
；
解得v=
；
故答案为：
．
气体分子运动时间为：t=
| R-r |
| v |
| S |
| ωr |
两个运动同时发生，故t=
| R-r |
| v |
| S |
| ωR |
解得v=
| (R-r)Rω |
| S |
故答案为：
| (R-r)Rω |
| S |
点评：本题关键是根据两个物体的直线运动和转动同时发生，时间相等，然后根据速度和线速度的定义列式求解．
练习册系列答案
相关题目
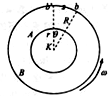1920年科学家斯特恩测定气体分子速率的装置如图所示，A、B为一双层共轴圆筒形容器，外筒半径为R内筒半径为r，可同时绕其几何轴经同一角速度ω高速旋转，其内部抽成真空．沿几何轴装有一根镀银的铂丝K，在铂丝上通电使其加热，银分子（即原子）蒸发成气体，其中一部分分子穿过A筒的狭缝a射出到达B筒的内表面．由于分子由内筒到达外筒需要一定时间．若容器不动，这些分子将到达外筒内壁上的b点，若容器转动，从a穿过的这些分子仍将沿原来的运动方向到达外筒内壁，但容器静止时的b点已转过弧长s到达b’点．（1）这个实验运用了
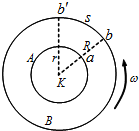1920年科学家斯特恩测定气体分子速率的装置如图所示，A、B为一双层共轴圆筒形容器，外筒半径为R，内筒半径为r，可同时绕其几何轴经同一角速度ω高速旋转，其内部抽成真空．沿几何轴装有一根镀银的铂丝K，在铂丝上通电使其加热，银分子（即原子）蒸发成气体，其中一部分分子穿过A筒的狭缝a射出到达B筒的内表面．由于分子由内筒到达外筒需要一定时间．若容器不动，这些分子将到达外筒内壁上的b点，若容器转动，从a穿过的这些分子仍将沿原来的运动方向到达外筒内壁，但容器静止时的b点已转过弧长s到达b’点．
