题目内容
【题目】如图所示,沿水平方向做匀变速直线运动的车厢中,悬挂小球的悬线偏离竖直方向的夹角θ=37°,小球和车厢相对静止,小球的质量为1kg (sin 37°=0.6,cos 37°=0.8,取g=10m/s2).求: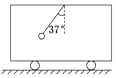
⑴车厢运动的加速度并说明车厢的运动情况;
⑵悬线对小球的拉力大小.
【答案】解:法一:合成法
⑴由于车厢沿水平方向运动,所以小球有水平方向的加速度,所受合力F沿水平方向.选小球为研究对象,受力分析如图所示.
![]()
由几何关系可得 F=mgtan θ
则得,小球的加速度 a= ![]() =gtan θ=10×tan37°=7.5 m/s2,方向向右,则车厢做向右的匀加速直线运动或向左的匀减速直线运动.
=gtan θ=10×tan37°=7.5 m/s2,方向向右,则车厢做向右的匀加速直线运动或向左的匀减速直线运动.
⑵悬线对球的拉力大小为FT= ![]() =
= ![]() N=12.5 N.
N=12.5 N.
法二:正交分解法
以水平向右为x轴正方向建立坐标系,并将悬线对小球的拉力FT正交分解,如图所示.
则沿水平方向有 FTsin θ=ma
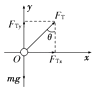
竖直方向有 FTcos θ﹣mg=0
联立解得 a=7.5 m/s2,FT=12.5 N
且加速度方向向右,故车厢做向右的匀加速直线运动或向左的匀减速直线运动.
答:(1)车厢运动的加速度是7.5 m/s2,方向向右.车厢做向右的匀加速直线运动或向左的匀减速直线运动.(2)悬线对小球的拉力大小是12.5N.
【解析】(1)对小球进行受力分析,根据牛顿第二定律求出加速度,而车厢相对于小球静止,加速度相等,进而判断车厢的运动情况;(2)根据力的合成与分解求出悬线的拉力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目