题目内容
两个质量相同的小球用不可伸长的细线连结，置于场强为E的匀强电场中，小球1和2均带正电．电荷量分别为q1和q2(q1>q2)．将细线拉直并使之与电场方向平行，如图所示，若将两小球同时从静止状态释放，则释放后细线中的张力F为(不计重力及两小球间的库仑力)( )
A．F＝
(q1－q2)E B．F＝(q1－q2)E
C．F＝ (q1＋q2)E D．F＝(q1＋q2)E
【答案】
A
【解析】
试题分析：对球1、2整体受力分析，根据牛顿第二定律得：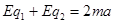
，
对球2受力分析，由牛顿第二定律得：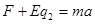
，两式联立得F＝
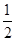(q1－q2)E，A正确，
考点：考查了电场和牛顿定律的综合应用
点评：解决本题关键在于把牛顿第二定律和电场力知识结合起来，在研究对象上能学会整体法和隔离法的应用．
练习册系列答案
相关题目
（2007?宁夏）两个质量相同的小球用不可伸长的细线连接，置于场强为E的匀强电场中，小球1和小球2均带正电，电量分别为q1和q2（q1＞q2）．将细线拉直并使之与电场方向平行，如图所示．若将两小球同时从静止状态释放，则释放后细线中的张力T为（不计重力及两小球间的库仑力）（ ）
两个质量相同的小球用不可伸长绝缘的细线连结，置于场强为E的匀强电场中，小球1带正电，电量为2q，小球2带负电，电量大小为q．将细线拉直并使之与电场方向平行，如图所示．若将两小球同时从静止状态释放，则释放后细线中的张力T为（不计重力及两小球间的库仑力）（ ）
（2013?虹口区二模）两个质量相同的小球用不可伸长的细线连结，置于场强为E的匀强电场中，小球1和小球2均带正电，电量分别为q1和q2（q1＞q2），两小球间的库仑力大小为F．将细线拉直并使之与电场方向平行，如图所示．若将两小球同时从静止状态释放，则释放后细线中的张力T为（不计重力）（ ）
和
（
（