题目内容
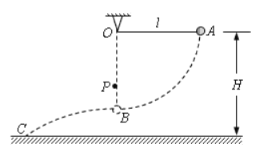
【题目】如图所示,一长L=0.45 m 的轻绳一端固定在O点,另一端连接一质量m=0.10 kg 的小球,悬点O距离水平地面的高度H=0.90 m.开始时小球处于A点,此时轻绳拉直处于水平方向上,让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P之前拉力F=3N,之后立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10 m/s2.
(1)轻绳断裂后小球从B点抛出并落在水平地面的C点,求C点与B点之间的水平距离;
(2)若OP=0.30 m,轻绳碰到钉子P时绳中拉力达到所能承受的最大拉力而断裂,求轻绳所能承受的最大拉力.
【答案】(1)0.90 m;(2)7 N.
【解析】
(1)设小球运动到B点时的速度大小vB,由机械能守恒定律得
![]()
小球从B点做平抛运动,由运动学规律得,水平方向上
![]()
竖直方向上
![]()
解得C点与B点之间的水平距离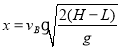 =0.90 m
=0.90 m
(2)若轻绳碰到钉子时,轻绳拉力恰好达到最大值Fm,由牛顿第二定律得
![]()
![]() (d为OP的长度)
(d为OP的长度)
联立解得![]()

练习册系列答案
相关题目