题目内容
 如图所示,相距20cm的平行金属导轨所在平面与水平面夹角θ=37°,现在导轨上放一质量为330g的金属棒ab,它与导轨间动摩擦因数为0.5,整个装置处于磁感应强度为2T的竖直向上匀强磁场中,导轨所接电源的电动势为15V,内阻不计,滑动变阻器的阻值满足要求,其他部分电阻不计,g取10m/s2,为了保证ab处于静止状态(cosθ=0.8),则:
如图所示,相距20cm的平行金属导轨所在平面与水平面夹角θ=37°,现在导轨上放一质量为330g的金属棒ab,它与导轨间动摩擦因数为0.5,整个装置处于磁感应强度为2T的竖直向上匀强磁场中,导轨所接电源的电动势为15V,内阻不计,滑动变阻器的阻值满足要求,其他部分电阻不计,g取10m/s2,为了保证ab处于静止状态(cosθ=0.8),则:(1)ab通入的最大电流为多少?
(2)ab通入的最小电流为多少?
(3)R的调节范围多大?
分析:本题(1)的关键是对导体棒ab进行受力分析并画出侧视图(注意安培力方向与磁场垂直),明确电流最大时,最大静摩擦力方向应沿导轨向下然后根据平衡条件列式即可求解;题(2)的关键是明确电流最小时,最大静摩擦力方向应沿导轨向上;题(3)的关键是根据闭合电路欧姆定律求出对应的最大电阻和最小电阻即可.
解答:解:(1)画出导体棒的侧视图,当电流最大时,最大静摩擦力方向应沿导轨向下,导体棒的受力分析如图所 示,根据平衡条件应有:
示,根据平衡条件应有:
Lcos37°=mgsin37°+
=mgcos37°
联立以上两式解得:
=16.5A
(2)当ab中电流最小时,导体棒所受的最大静摩擦力方向沿导轨向下,根据平衡条件应有:
BIL+
=mgsin37°
=mgcos37°
联立以上两式解得:I=1.5A
(3)根据闭合电路欧姆定律I=
可知,变阻器的最大电阻为:
=
=
Ω=10Ω
最小电阻为:
=
=
Ω=0.9Ω
所以,若是导体棒静止在导轨上,变阻器的电阻调节范围是0.9~10Ω
答:(1)ab通入的最大电流为16.5A;
(2)ab通入的最小电流为1.5A;
(3)R的调节范围是0.9~10Ω.
 示,根据平衡条件应有:
示,根据平衡条件应有:
|
| μF | N |
| F | N |
联立以上两式解得:
| I | m |
(2)当ab中电流最小时,导体棒所受的最大静摩擦力方向沿导轨向下,根据平衡条件应有:
BIL+
| μF | N |
| F | N |
联立以上两式解得:I=1.5A
(3)根据闭合电路欧姆定律I=
| E |
| R |
| R | max |
| E |
| I |
| 15 |
| 1.5 |
最小电阻为:
| R | min |
| E | ||
|
| 15 |
| 16.5 |
所以,若是导体棒静止在导轨上,变阻器的电阻调节范围是0.9~10Ω
答:(1)ab通入的最大电流为16.5A;
(2)ab通入的最小电流为1.5A;
(3)R的调节范围是0.9~10Ω.
点评:遇到有关导轨问题,关键是画出侧视图,然后对导体棒进行正确进行受力分析,然后运用平衡条件或牛顿第二定律求解即可.

练习册系列答案
相关题目
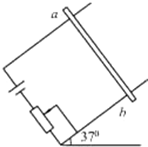 如图所示,相距20cm的两根光滑平行铜导轨,导轨平面倾角为a=37°,上面放着质量为80g的金属杆ab,整个装置放在B=0.2T的匀强磁场中.
如图所示,相距20cm的两根光滑平行铜导轨,导轨平面倾角为a=37°,上面放着质量为80g的金属杆ab,整个装置放在B=0.2T的匀强磁场中.
 ,现在导轨上放一质量为330g的金属棒ab,它与导轨间动摩擦因数为0.50,整个装置处于磁感应强度为2T的竖直向上匀强磁场中,导轨所接电源的电动势为15V,电阻不计,滑动变阻器的阻值满足要求,其他部分电阻不计,取
,现在导轨上放一质量为330g的金属棒ab,它与导轨间动摩擦因数为0.50,整个装置处于磁感应强度为2T的竖直向上匀强磁场中,导轨所接电源的电动势为15V,电阻不计,滑动变阻器的阻值满足要求,其他部分电阻不计,取 ,为了保证ab处于静止状态,则:
,为了保证ab处于静止状态,则:
