题目内容
6.如图甲,质量为m=1kg的小木块左端与轻弹簧相连,弹簧的另一端与固定在足够大的光滑水平桌面上的挡板相连,木块的右端与一轻细线连接,细线绕过光滑的质量不计的轻滑轮,木块处于静止状态.在下列情况中弹簧均处于弹性限度内,不计空气阻力及线的形变,重力加速度为g.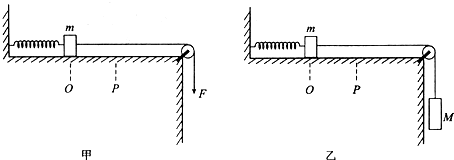
(1)图甲中,在线的另一端施加一竖直向下的大小为F=10N的恒力,木块离开初始位置O由静止开始向右运动,弹簧开始发生伸长形变,已知木块过P点时,速度大小为V=2m/s,O、P两点间距离为s=0.4m.求木块拉至P点时弹簧的弹性势能;
(2)如果在线的另一端不是施加恒力,而是悬挂一个质量为M=3kg的物块,如图乙所示,木块也从初始位置O由静止开始向右运动,求木块通过P点时的动能.
分析 (1)用力F拉木块至P点,根据功能关系求解
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,由机械能守恒定律列出等式求解.
解答 解:(1)用力F拉木块至P点时,设此时弹簧的弹性势能为EP,根据功能关系有:
$Fs={E}_{p}+\frac{1}{2}m{v}^{2}$,
代入数据解得:Ep=2J.
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,设木块的速度为v′,由机械能守恒定律得:
$Mgs={E}_{p}+\frac{1}{2}(M+m)v{′}^{2}$,
代入数据得:v′=$\sqrt{5}$m/s,
木块通过P点时的动能为:${E}_{k}=\frac{1}{2}mv{′}^{2}=\frac{1}{2}×1×5J=2.5J$.
答:(1)木块拉至P点时弹簧的弹性势能为2J;
(2)木块通过P点时的动能为2.5J.
点评 正确受力分析,明确各种功能关系,是解答这类问题的关键,这类问题对于提高学生的分析综合能力起着很重要的作用.

练习册系列答案
相关题目
16.从1907年起,美国物理学家密立根开始以精湛的技术测量光电效应中的几个重要物理量.表是按照密立根的方法进行实验时得到的某金属的遏止电压Uc和入射光的频率ν的几组数据.
(1)在给出的坐标纸中作出Uc-ν图象;
(2)根据所作图象求出该金属的截止频率νc;(结果保留三位有效数字)
(3)根据图象求出普朗克常量的值.(结果保留两位有效数字)
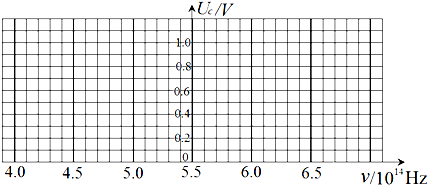
| Uc/V | 0.54 | 0.64 | 0.71 | 0.81 | 0.88 |
| ν/1014Hz | 5.64 | 5.89 | 6.10 | 6.30 | 6.50 |
(2)根据所作图象求出该金属的截止频率νc;(结果保留三位有效数字)
(3)根据图象求出普朗克常量的值.(结果保留两位有效数字)

17.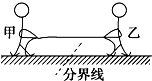 如图,甲、乙两人在粗糙程度相同的水平地面上进行拔河比赛,两人中间位置处有一分界线,最后甲先使乙越过分界线,甲赢.若绳子质量不计,下列说法正确的是( )
如图,甲、乙两人在粗糙程度相同的水平地面上进行拔河比赛,两人中间位置处有一分界线,最后甲先使乙越过分界线,甲赢.若绳子质量不计,下列说法正确的是( )
 如图,甲、乙两人在粗糙程度相同的水平地面上进行拔河比赛,两人中间位置处有一分界线,最后甲先使乙越过分界线,甲赢.若绳子质量不计,下列说法正确的是( )
如图,甲、乙两人在粗糙程度相同的水平地面上进行拔河比赛,两人中间位置处有一分界线,最后甲先使乙越过分界线,甲赢.若绳子质量不计,下列说法正确的是( )| A. | 甲比乙拉着绳子的力要大 | |
| B. | 每个人拉着绳子的力的大小是相等的 | |
| C. | 地面对甲比对乙的静摩擦力要大一些 | |
| D. | 甲的体重一定比乙的体重大 |
14.下列说法中正确的是( )
| A. | 参考系只能选择静止不动的物体 | |
| B. | 研究物体的运动时,只有选择好参考系后,物体的运动才能确定 | |
| C. | 同一运动的物体,如果选择了不同的参考系,观察的结果可能不同 | |
| D. | 我们通常所说的楼房静止不动,是指楼房相对地球的位置没有变化 |
16.关于质点的描述,下列说法中正确的是( )
| A. | 质点就是很小的点 | |
| B. | 只有质量很小、体积很小的物体才可以看作质点 | |
| C. | 只有静止的物体才能看作质点 | |
| D. | 自然界中一切物体都是有大小的,所以质点是一种理想化模型 |
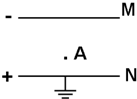 如图所示,是一对彼此绝缘相距d=5cm的平行金属带电极板MN,N板接地,在两极板MN间距离M板3.5cm的A点有一带电量为q=4×10-6C的带电液滴,其质量m=4×10-4kg,恰好处于静止状态.求:
如图所示,是一对彼此绝缘相距d=5cm的平行金属带电极板MN,N板接地,在两极板MN间距离M板3.5cm的A点有一带电量为q=4×10-6C的带电液滴,其质量m=4×10-4kg,恰好处于静止状态.求: