题目内容
19.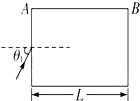 折射率为n、长度为L的玻璃纤维置于空气中,若从A端射入的光线能在玻璃纤维中发生全反射,最后从B端射出,如图所示,求:
折射率为n、长度为L的玻璃纤维置于空气中,若从A端射入的光线能在玻璃纤维中发生全反射,最后从B端射出,如图所示,求:(1)光在A面上入射角的最大值.
(2)若光在纤维中恰能发生全反射,由A端射入到从B端射出经历的时间是多少?
(3)若要使从A端射入的光线不论入射角多大,都能在纤维中发生全反射,而从B端射出,纤维的折射率不能小于多少?
分析 (1)光线在光纤侧面恰好发生全反射时,入射角等于临界角C,光在A面上入射角最大,先根据公式sinC=$\frac{1}{n}$,求出临界角C,再由几何关系求出光线在A端面的折射角,即可由折射率公式求解入射角的最大值.
(2)由数学知识求出从左端射入到右端射出光线通过的路程x.光在光纤中的传播速度为v=$\frac{c}{n}$,由t=$\frac{x}{v}$求解时间.或求出光在沿纤维轴线方向上的速度分量求解时间.
(3)当当入射角θ1=90°时,折射率最小.
解答  解:(1)光路如图,要在纤维中发生全反射,其临界角C,有 sin$C=\frac{1}{n}$
解:(1)光路如图,要在纤维中发生全反射,其临界角C,有 sin$C=\frac{1}{n}$
折射角 θ2=90°-C
所以cos${θ_2}=\frac{1}{n}$,sin${θ_2}=\frac{{\sqrt{{n^2}-1}}}{n}$
由折射定律:sinθ1=nsin${θ_2}=\sqrt{{n^2}-1}$
故入射角的最大值 θ1=arcsin$\sqrt{{n^2}-1}$.
(2)光在纤维中传播的速度$v=\frac{c}{n}(c$为光在真空中传播的速度)
光在沿纤维轴线方向上的速度分量 v1=vcos${θ_2}=\frac{v}{n}=\frac{c}{n^2}$
所用时间:$t=\frac{L}{v_1}=\frac{{{n^2}L}}{c}$.
(3)当入射角θ1=90°时,由(1)得$n=\sqrt{2}$.
答:
(1)光在A面上入射角的最大值是arcsin$\sqrt{{n^2}-1}$.
(2)若光在纤维中恰能发生全反射,由A端射入到从B端射出经历的时间是$\frac{{n}^{2}L}{c}$.
(3)纤维的折射率不能小于 $\sqrt{2}$.
点评 是对于几何光学问题,一定要画出光路图,并根据题意找出临界角与其他角度的关系,再结合相应的规律解题.

| A. | 不可能看作质点的两物体之间不存在相互作用的引力 | |
| B. | 可看作质点的两物体间的引力可用F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$计算 | |
| C. | 由F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$可知,两物体间距离r减小时,它们之间的引力增大,紧靠在一起时,万有引力非常大 | |
| D. | 引力常量的大小首先是由卡文迪许测出来的 |
 如图所示,MN、PQ为同一水平面内的两平行导轨,导轨间有垂直于导轨平面的磁场,导体ab、cd与导轨有良好的接触并能自由滑动,当ab沿轨道向左滑动时,则( )
如图所示,MN、PQ为同一水平面内的两平行导轨,导轨间有垂直于导轨平面的磁场,导体ab、cd与导轨有良好的接触并能自由滑动,当ab沿轨道向左滑动时,则( )| A. | cd左滑 | B. | cd不动 | C. | cd右滑 | D. | 无法确定 |
 如图所示,一根长导线弯成“n”形,通以直流电I,正中间用不计长度的一段绝缘线悬挂一金属环C,环与导线处于同一竖直平面内,在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯成“n”形,通以直流电I,正中间用不计长度的一段绝缘线悬挂一金属环C,环与导线处于同一竖直平面内,在电流I增大的过程中,下列叙述正确的是( )| A. | 金属环C中无感应电流产生 | |
| B. | 金属环C中有沿逆时针方向的感应电流产生 | |
| C. | 悬挂金属环C的竖直线拉力变大 | |
| D. | 金属环C仍能保持静止状态 |
| A. | 摩擦起电,是因为摩擦导致电子从一个物体转移到另一个物体而形成的 | |
| B. | 在电场中无论移动正电荷还是负电荷,只要电场力做正功,电荷电势能一定要减少 | |
| C. | 在地毯中夹杂导电纤维是为了利用人在地毯上行走时摩擦产生的静电 | |
| D. | 电势降低的方向,一定就是场强方向 |
| A. | 1号箱在2号箱的正下方 | B. | 两箱的水平距离保持不变 | ||
| C. | 两箱的水平距离越来越大 | D. | 两箱的水平距离越来越小 |


