��Ŀ����
����Ŀ��С�͵����������ں���վ�ϣ�һ��������������Բ���˶��������뾶Ϊ����뾶��3����ijʱ�̣�����վʹ���������ٷ��룬����������ͼ��ʾ����Բ������£���������涺��һ��ʱ����ɿƿ�������������������ԭ��Բ������أ�����һ�λص������ʱǡ�뺽��վ�Խӣ���������������ʱ����Ժ��Բ��ƣ����������к���վ����ԭ����������С���֪���������������ٶ�Ϊg������뾶ΪR��������������ת��Ӱ�죬�������������������ͣ�������ʱ��ԼΪ�� ��

A. ![]()
B. ![]()
C. ![]()
D. ![]()
���𰸡�B
����������������ͺ���ɻ��ڰ뾶3R�Ĺ��������ʱ������ΪT��������������Բ���˶�������Ӧ��ţ�ٵڶ�������![]() ��
�� ![]() ������
������![]()
�������������������������Ƶ������������� ![]() ������
������![]() �������������С��Բ������е�������T1������ɻ��ڴ�Բ������е�������T2���Ե������ͺ���ɻ����ݿ����յ������ɷֱ���
�������������С��Բ������е�������T1������ɻ��ڴ�Բ������е�������T2���Ե������ͺ���ɻ����ݿ����յ������ɷֱ���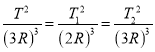 ����Ϊʹ����������ԭ��Բ����ص�������뺽��ɻ�ʵ�ֶԽӣ�������������������涺����ʱ��tӦ����
����Ϊʹ����������ԭ��Բ����ص�������뺽��ɻ�ʵ�ֶԽӣ�������������������涺����ʱ��tӦ����![]() �������У�n=1��2��3��������
��������n=1��2��3��������
�����٢ڢ���![]() �����У�n=1��2��3����������n=1ʱ��������������������ͣ����ʱ����̣���
�����У�n=1��2��3����������n=1ʱ��������������������ͣ����ʱ����̣���![]() ����B��ȷ��ACD����
����B��ȷ��ACD����
��ѡB��

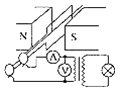
����Ŀ��Ϊ����̽�����ٶ������������Ĺ�ϵ�������ṩ��ͼ����ʾ��ʵ��װ�ã�

��1������ʵ�������ȷ����
A����ľ�岻�����ֵ�һ���ʵ���ߣ�ʹС�������뼰�����̵�ǣ����ǡ���������˶� |
B�����ڻ��ֵĸ߶ȣ�ʹϸ����ľ��ƽ�� |
C���Ƚ�ͨ��Դ���ͷ�С�� |
D��ʵ����С���ļ��ٶ�Խ��Խ�� |
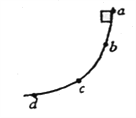
��2����ʵ���У��õ�һ����ͼ����ʾ��ֽ������֪���ڼ�������ʱ����ΪT=0.1S���Ҽ��x1��x2��x3��x4��x5��x6�������ֱ�Ϊ3.09cm��3.43cm��3.77cm��4.10cm��4.44cm��4.77cm����С���ļ��ٶ�a= m/s2�����������λ��Ч���֣���

��3����һ��ͬѧ����С�������е���������һ����̽�����ٶ�a����������F�Ĺ�ϵ�������ڹ��ˮƽ����б��������·ֱ�����ʵ�飬�õ�������a��Fͼ�ߣ���ͼ����ʾ��ͼ�� ���ڹ����б����µõ��ģ������١������ڡ�����С�������������������m= kg��

����Ŀ��ij����ʵ��С�����������Ľ���ʵ�����һ������Ԫ���ķ�����������,�������ݼ�¼�ڱ�����:
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
U/V | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.6 | 2.8 | 3.0 |
I/mA | 0 | 0.9 | 2.2 | 4.2 | 6.7 | 11.9 | 19.0 | 23.8 | 30.0 | 37.1 |
������:
A.����Ԫ��Rx
B.������A(0~50mA,����ԼΪ200��)
C.��ѹ��V1(0~3V,����ԼΪ10k��)
D.��ѹ��V2(0~6V,����ԼΪ15��)
E.����������R1(0~20��,2A)
F.����������R2(0~200��,0.2A)
G.ѧ����Դ(ֱ��4V)
H.���ؼ�����
��1��Ϊ�˵��ڷ���,������ȷ����,��ѹ��Ӧѡ_______,����������Ӧѡ_______.(���������)
��2�������߿��ڻ���ʵ���·ͼ_____________________.
��3��������ֽ������㷨����Ԫ���ķ�������(I~U)����______________.