��Ŀ����
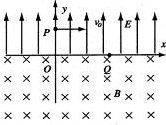
��ͼ��ʾ��x���Ϸ���һ��ǿ�糡��������y��ƽ�У�x���·���һ��ǿ�ų�������ֱֽ�����һ����Ϊm������Ϊ-q��q��0�����������ٶ�v0��y���ϵ�P��ƽ��x�᷽������糡��x���ϵ�O�����ų�����������ԭ��O�뿪�ų�����֪OP=L��OQ=2L������������һ����������
��1�����ӵ���Q��ʱ���ٶȴ�С�ͷ���
��2�������ڴų����˶��Ĺ���뾶��
��3�������ڴų��е��˶�ʱ�䣮
��1�����ӵ���Q��ʱ���ٶȴ�С�ͷ���
��2�������ڴų����˶��Ĺ���뾶��
��3�������ڴų��е��˶�ʱ�䣮

��1���������ڵ糡���˶�ʱ��Ϊt1������Qʱ��ֱ���ٶ�Ϊvy���ٶȴ�СΪv��������x��н�Ϊ�ȣ����˶�ѧ��ʽ�ã�
ˮƽ�����У�2L=v0t1
��ֱ�����У�L=
t0
������ã�vy=v0��
�� v=
=
v0
tan��=
=1���æ�=45��
��2�������ڴų��еĹ켣��ͼ��ʾ���ɼ��ι�ϵ�ɵ������ڴų��еĹ���뾶��R=
=
?2L=
L
��3����ͼ֪�������ڴų��е��˶�ʱ�켣��Ӧ��Բ�Ľ�Ϊ270�㣬���ڴų����˶���ʱ�䣺
t2=
=
T
��Բ���˶�֪ʶ�ã�T=
=
v0=
�ʵ� t2=
T=
��
=
�𣺣�1�����ӵ���Q��ʱ���ٶȴ�СΪ
v0��������x���45��б���£�
��2�������ڴų����˶��Ĺ���뾶Ϊ
L��
��3�������ڴų��е��˶�ʱ��
��

ˮƽ�����У�2L=v0t1
��ֱ�����У�L=
| vy |
| 2 |
������ã�vy=v0��
�� v=
| v02+vy2 |
| 2 |
tan��=
| vy |
| v0 |
��2�������ڴų��еĹ켣��ͼ��ʾ���ɼ��ι�ϵ�ɵ������ڴų��еĹ���뾶��R=
| ||
| 2 |
| . |
| OQ |
| ||
| 2 |
| 2 |
��3����ͼ֪�������ڴų��е��˶�ʱ�켣��Ӧ��Բ�Ľ�Ϊ270�㣬���ڴų����˶���ʱ�䣺
t2=
| 270�� |
| 360�� |
| 3 |
| 4 |
��Բ���˶�֪ʶ�ã�T=
| 2��R |
| v |
2��
| ||
|
| 2��L |
| v0 |
�ʵ� t2=
| 3 |
| 4 |
| 3 |
| 4 |
| 2��L |
| v0 |
| 3��L |
| 2v0 |
�𣺣�1�����ӵ���Q��ʱ���ٶȴ�СΪ
| 2 |
��2�������ڴų����˶��Ĺ���뾶Ϊ
| 2 |
��3�������ڴų��е��˶�ʱ��
| 3��L |
| 2v0 |


��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ