题目内容
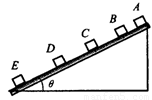
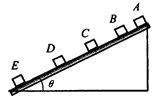
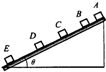 一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物体下滑加速度
一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物体下滑加速度4.90
4.90
m/s2,若此斜面的倾角θ为37°,则物块与斜面间的动摩擦因数为0.125
0.125
.(取g=9.80m/s2,sin37°=0.600,cos37°=0.800,保留3位有效数字)分析:根据匀变速直线运动的推论△x=aT2,利用逐差法求解物体的加速度.再根据牛顿第二定律求出物块与斜面间的动摩擦因数.
解答:解:设AB=x1,BC=x2,CD=x3,DE=x4.则有
x3-x1=2a1T2
x4-x2=2a2T2
物体的加速度a=
(a1+a2)=
,其中T=0.1s
代入解得,a=4.90m/s2
根据牛顿第二定律得,mgsin37°-μmgcos37°=ma
代入解得,μ=0.125.
故答案为:4.90,0.125
x3-x1=2a1T2
x4-x2=2a2T2
物体的加速度a=
| 1 |
| 2 |
| (x3+x4)-(x1+x2) |
| 4T2 |
代入解得,a=4.90m/s2
根据牛顿第二定律得,mgsin37°-μmgcos37°=ma
代入解得,μ=0.125.
故答案为:4.90,0.125
点评:本题中频闪照相与打点计时器作用相似,每隔一定时间记录一次物体的位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物块经过D点时的速度大小为
一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物块经过D点时的速度大小为