题目内容
19.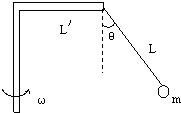 如图所示,已知绳长L=0.5m,水平杆L′=0.3m,小球质量m=0.3kg,整个装置可绕竖直轴匀速转动,问:(sin37°=0.6,cos37°=0.8,g=10m/s2,结果均保留三位有效数字)
如图所示,已知绳长L=0.5m,水平杆L′=0.3m,小球质量m=0.3kg,整个装置可绕竖直轴匀速转动,问:(sin37°=0.6,cos37°=0.8,g=10m/s2,结果均保留三位有效数字)(1)要使绳子与竖直方向成θ=37°角,该装置必须以多大的角速度转动才行?
(2)此时绳子的张力多大?
分析 (1)当绳子与竖直方向成θ=37°角时,对小球进行受力分析,找出向心力,结合几何知识找出转动的半径,即可得知所需要的加速度.
(2)小球在做匀速圆周运动时,在竖直方向上合力为零,结合三角形的知识可解的此时绳子的张力.
解答 解:(1)当绳子与竖直方向成θ=37°角时,对小球进行受力分析,受重力和绳子的拉力作用,水平方向上合力提供向心力,如图,则有:
$tanθ=\frac{{F}_{向}}{mg}$…①
设做圆周运动半径为r,加速度为ω,则有:
${F}_{向}=m{ω}^{2}r$…②
r=L′+Lsinθ…③
联立①②③式并代入数据得:$ω=\frac{5}{2}\sqrt{2}rad/s$
(2)通过对小球的受力分析可知,在竖直方向上合力为零,则有:$cosθ=\frac{mg}{{F}_{拉}}$…④
代入数据得:F拉=3.75N
答:(1)要使绳子与竖直方向成θ=37°角,该装置必须以$\frac{5}{2}\sqrt{2}$rad/s的角速度转动才行.
(2)此时绳子的张力为3.75N.
点评 解答该题的关键是正确的对小球进行受力分析,确定向心力.向心力是沿半径方向上的所有力的合力,该类型的题,在竖直方向上合力为零,由此可方便的寻找绳子的拉力与重力的关系.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
3.在下列关于近代物理知识的说法中,正确的是( )
| A. | α粒子散射实验是卢瑟福建立原子核式结构模型的重要依据 | |
| B. | 光电效应和康普顿效应深入揭示了光的粒子性,前者表明光子具有能量,后者表明光子除了具有能量外还具有动量 | |
| C. | 根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动速度减小 | |
| D. | 在核反应中元素的种类不会改变 | |
| E. | ${\;}_{83}^{210}$Bi的半衰期是5天,12g${\;}_{83}^{210}$Bi经过15天后还有1.5g未衰变 |
7.关于弹力的方向,以下说法正确的是( )
| A. | 压力的方向总是垂直于接触面,并指向被压物 | |
| B. | 支持力的方向总是垂直于支持面,并指向被支持物 | |
| C. | 绳对物体拉力的方向总是沿着绳,并指向绳收缩的方向 | |
| D. | 杆对物体的弹力总是沿着杆,并指向杆收缩的方向 |
8.电磁波在真空中的传播速度为c,若某电磁波的频率为f,则该电磁波在真空中的波长为( )
| A. | $\frac{c}{f}$ | B. | $\frac{1}{cf}$ | C. | $\frac{f}{c}$ | D. | cf |
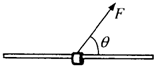 如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.对环施加F=9N与杆夹角θ=53°位于竖直平面内斜向上的拉力,使圆环以a=4.4m/s2的加速度沿杆运劝,求环与杆间动摩擦因数μ的大小.(重力加速度g取10m/s2)
如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.对环施加F=9N与杆夹角θ=53°位于竖直平面内斜向上的拉力,使圆环以a=4.4m/s2的加速度沿杆运劝,求环与杆间动摩擦因数μ的大小.(重力加速度g取10m/s2) 如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问:
如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问: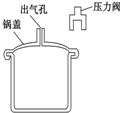 1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住(如图).当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3cm,外界大气压为1.0×105Pa,温度为20℃,要使高压锅内的温度达到120℃,则限压阀的质量应为多少?
1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住(如图).当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3cm,外界大气压为1.0×105Pa,温度为20℃,要使高压锅内的温度达到120℃,则限压阀的质量应为多少?