题目内容
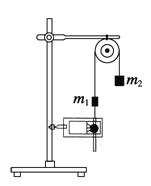
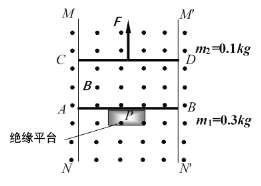
【题目】如图所示,MN和M′N′是两根互相平行、竖直固定、足够长的光滑金属导轨,两根导体棒AB和CD质量分别为m1=0.3kg和m2=0.1kg,均与导轨垂直接触。开始AB棒放在绝缘平台P上,t=0时CD棒开始受到竖直向上的恒力F=4N,从静止开始向上运动,t=2s时CD棒的速度为v0=2m/s,此时快速撤离绝缘平台P。已知AB棒的电阻为R1=0.5Ω,CD棒的电阻为R2=1.5Ω,导轨间距为L=0.5m。整个装置处在磁感应强度为B=2T的匀强磁场中,磁场方向与导轨所在平面垂直。两导体棒始终与导轨接触良好,导轨电阻不计,重力加速g取10m/s2。求:
(1)撤去绝缘平台前瞬间,CD棒哪端电势高,两端电压U;
(2)0~2s时间内,CD棒这段时间内上升的距离h;
(3)撤离绝缘平台后,AB棒和CD棒分别达到的最大速度大小v1和v2。
【答案】(1)0.5V;(2)11.6m;(3)1m/s,5m/s
【解析】
(1)撤去平台前,AB棒静止,CD切割磁感线产生电动势E1,在t=2s时,由法拉第电磁感应定律,D点电势高
E1=BLv0
由闭合电路欧姆定律
![]()
U=(E1-I1R2)
解得
U=0.5V
(2)在0~2s内,对CD棒,由动量定理
Ft-m2gt–IA=m2v0-0
由安培力公式FA=BIL,由闭合电路欧姆定律
![]()
由法拉第电磁感应定律
![]()
由冲量公式
![]()
其中h为CD棒在该时间内上升的高度
得
h=11.6m
(3)撤去平台后,AB棒做加速度减小的加速下落,CD棒继续加速度减小的加速上升,由牛顿第二定律得,对AB棒
m1g-BIL=m1a1
对CD棒
F-m2g-BIL=m2a2
得
F-m1g-m2g=m2a2-m1a1
由于
![]()
所以
m2a2-m1a1=0
所以当a2=0时,a1=0,也就是两棒最终同时开始做匀速运动,对AB棒和CD棒组成的系统,由于合外力为零,系统动量守恒,取向上方向为正方向
m2v0+0=m2v2+m1(-v1)
由法拉第电磁感应定律得
E=BL(v1+v2)
解得
v1=1m/s,v2=5m/s

【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为![]() ,完成下面问题。
,完成下面问题。

(1)根据打点计时器打出的纸带,我们可以直接得到的物理量是
A.时间间隔 | B.加速度 |
C.瞬时速度 | D.平均速度 |
(2)根据纸带上各个测量点间的距离,某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算
并填入表中,请你将4点对应的时刻的瞬时速度填入表中;(要求保留3位有效数字)
瞬时速度 | v1 | v2 | v3 | v4 | v5 |
数值(m/s) | 0.165 | 0.214 | 0.263 | 0.363 |
(3)在图所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线。
(4)由图像求出小车的加速度![]()