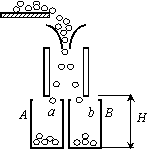题目内容
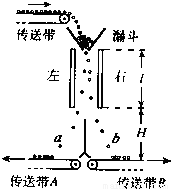
如图是某种静电分选器的原理示意图。两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场,分选器漏斗的出口与两板上端处于同一高度,到两板距离相等。混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电。经分选电场后,a、b两种颗粒分别落到水平传送带A、B上。已知两板间距d=0.1m,板的度![]() ,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为
,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为![]() 。设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计。要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量。重力加速度g取
。设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计。要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量。重力加速度g取![]() 。
。
(1)左右两板各带何种电荷?两极板间的电压多大?
(2)若两带电平行板的下端距传送带A、B的高度H=0.3m,颗粒落至传送带时的速度大小是多少?
(3)设颗粒每次与传送带碰撞反弹时,沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半。写出颗粒第n次碰撞反弹高度的表达式。并求出经过多少次碰撞,颗粒反弹的高度小于0.01m。
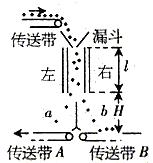
(1)![]()
(2)![]()
(3)4次
解析:
(1)左板带负电荷,右板带正电荷。依题意,颗粒在平行板间的竖直方向上满足![]()
在水平方向上满足:![]()
两式联立得![]()
(2)根据动能定理,颗粒落到水平传送带上满足
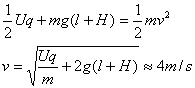
(3)在竖直方向颗粒作自由落体运动,它第一次落到水平传送带上沿竖直方向的速度
![]()
反弹高度![]()
根据题设条件,颗粒第n次反弹后上升的高度:
![]()
当![]() 时,
时,![]()

练习册系列答案
相关题目
 (2004?北京)如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.
(2004?北京)如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.