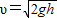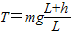题目内容
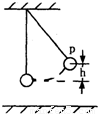
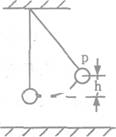
 如图所示,一小球用一长为L不可伸长的细线悬挂在天花板上,将小球从最低点拉至P点,并使细线保持绷直状态,然后在P点由静止释放,当小球经过最低点时细线恰好被拉断.重力加速度为g,不计空气阻力.则( )
如图所示,一小球用一长为L不可伸长的细线悬挂在天花板上,将小球从最低点拉至P点,并使细线保持绷直状态,然后在P点由静止释放,当小球经过最低点时细线恰好被拉断.重力加速度为g,不计空气阻力.则( )分析:小球向下运动的过程,细线的拉力不做功,机械能守恒,根据机械能守恒定律列式求解细线断前瞬间小球的速度大小;
细线断前瞬间,由重力和拉力的合力提供向心力,根据牛顿第二定律列式求解细线的拉力大小;
细线断后小球做平抛运动,是一种匀变速曲线运动.
细线断前瞬间,由重力和拉力的合力提供向心力,根据牛顿第二定律列式求解细线的拉力大小;
细线断后小球做平抛运动,是一种匀变速曲线运动.
解答:解:A、根据机械能守恒得:mgh=
mv2,得v=
.故A正确.
B、细线断前瞬间,由牛顿第二定律得:T-mg=m
,解得T=mg+mg
=mg
.故B错误.
C、D细线断后小球做平抛运动,加速度是g,是一种匀变速曲线运动.故C错误,D正确.
故选AD
| 1 |
| 2 |
| 2gh |
B、细线断前瞬间,由牛顿第二定律得:T-mg=m
| v2 |
| L |
| 2h |
| L |
| L+2h |
| L |
C、D细线断后小球做平抛运动,加速度是g,是一种匀变速曲线运动.故C错误,D正确.
故选AD
点评:本题是机械能守恒定律与牛顿第二定律的综合应用,常规题,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目