题目内容
【题目】如图所示,某同学利用电子秤、轻质材料做成的凹形轨道,研究小球通过凹形轨道的运动,由于小球质量远大于凹形轨道的质量,下面计算中可以忽略凹形轨道的质量,已知凹形轨道最下方为半径为R的圆弧轨道,重力加速度为g,
⑴把凹形轨道放在电子秤上,小球放在轨道最低点,电子秤读数为m1 .
⑵让小球从离轨道最低点H处由静止释放,当小球通过轨道最低点时,用手机抓拍出电子秤读数为m2 .
⑶根据电子秤两次读数可知,小球通过轨道最低点时的速度为 , 这说明小球通过凹形轨道最低点时处于(填“超重”“失重”或“平衡”)状态.
⑷小球从离轨道最低点高H处由静止释放到通过最低点的过程中克服摩擦力做功为 .
【答案】![]() ;超重;
;超重;![]()
【解析】解:(3)以小球为研究对象,根据牛顿第二定得:
FN﹣m1g=m1 ![]()
据题有:FN=m2g.
联立可得:v= ![]()
小球通过凹形轨道最低点时有向上的加速度,处于超重状态.(4)小球从离轨道最低点高H处由静止释放到通过最低点的过程中,由功能原理知,小球克服摩擦力做功等于小球机械能的减少,为:
Wf=m1gH﹣ ![]() =
= ![]() .
.
故答案为:(3) ![]() ,超重;(4)
,超重;(4) ![]() .
.
(3)以小球为研究对象,根据牛顿第二定律和向心力公式列式,可求得小球通过轨道最低点时的速度.根据小球的加速度方向分析其状态.(4)小球从离轨道最低点高H处由静止释放到通过最低点的过程中,重力做正功,摩擦力做负功,由功能原理求克服摩擦力做功.

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某实验小组正在测定一节新型电池的电动势(约为3V)和内阻,现要选取一个定值电阻R0当做保护电阻。
(1)首先为了准确测量定值电阻R0阻值,在操作台上准备了如下实验器材:
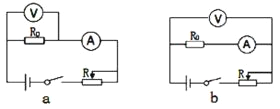
A.电压表V(量程3V,电阻约为4kΩ) |
B.电流表A1(量程1A,内阻约0.5Ω) |
C.电流表A2(量程3A,内阻约0.5Ω) |
D.定值电阻R0(阻值约为3Ω) |
E.滑动变阻器R(0-10Ω)
F.开关s一个,导线若干
根据上述器材,在测量R0阻值时应选择________(填序号)为电流表,其实验电路图应选择以下哪种接法________(填字母a或b),经测量定值电阻R0阻值为2.8Ω。
(2)之后为了测量该新型电池的电动势和内阻,设计了如下实验,在下图中将所选 器材进行连接。
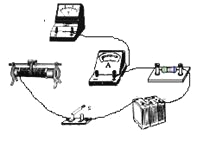
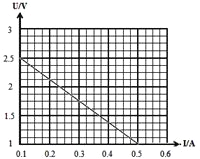
(3)根据实验记录做出U-I图线如图所示,从中可以求出待测新型电池的内阻为________Ω,电池电动势为________V(保留两位有效数字)。