Question

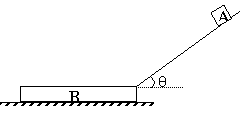
（12分）如图所示，一质量为2kg的木板B静止在光滑的水平面上，其右端上表面紧靠一固定斜面轨道的底端（斜面底端与木块B右端的上表面之间有一段小圆弧平滑连接)，轨道与水平面的夹角θ=37⁰，一质量也为2kg的物块A由距轨道底端8m处的斜面轨道上静止释放，物块A刚好没有从木板B的左端滑出，已知物块A与斜面轨道间的动摩擦因数均为0．25，与木板B上表面间的动摩擦因数均为0．2，sinθ=0．6，cosθ=0．8，g 取 10 m/s²，物块A可看作质点．请问：

（1）物块A刚滑上木板B时的速度有多大？

（2）木板B的长度为多少？

（3）物块A从开始下滑到相对木板B静止共经历了多长时间？

Answer 1

（12分）解：

（1）木块A从斜面滑下的加速度为

                                                   （2分)

木块A滑到木块B上时的速度为        

                                     

                                （2分)

（2）和（3）  木块A在木块B上滑动时，它们的加速度大小相等，数值为

                                           （2分)

设木块B的长度至少为L，两木块最终的共同速度为，在达到最大速度时，木块B滑行的距离为，根据题目所给条件可列方程：

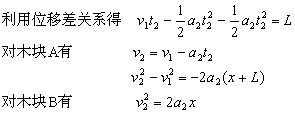                         （4分) 

联立解得相对滑行时间和木块B的长度分别为：

                                                                  （2分)