题目内容
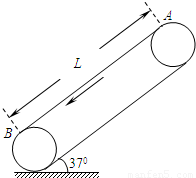
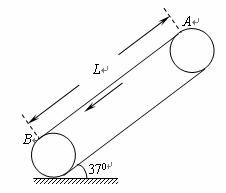
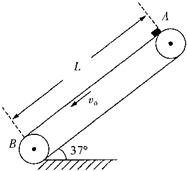 如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转动.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m小物块在皮带上滑过后会留下痕迹,求小物块离开皮带后,皮带上痕迹的长度.(sin37°=0.6,cos37°=0.8,g取10m/s2)
如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转动.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m小物块在皮带上滑过后会留下痕迹,求小物块离开皮带后,皮带上痕迹的长度.(sin37°=0.6,cos37°=0.8,g取10m/s2)分析:痕迹是由于物块和皮带的相对运动产生的,此相对运动由两个过程构成,一:物块速度小于传送带速度时,两者相对滑动,会出现划痕,此过程摩擦力向下,由牛顿第二定律可以得到加速度,进而由速度时间关系得到物块从运动到速度与传送带相等的时间,可算此阶段的相对位移,
二:物块速度超过传送带速度后,摩擦力向上,可由牛顿第二定律求得此时的加速度,进而计算离开传送带的时间,最后确定此阶段的相对位移.
两个阶段的相对位移之和就是总划痕的长度.
二:物块速度超过传送带速度后,摩擦力向上,可由牛顿第二定律求得此时的加速度,进而计算离开传送带的时间,最后确定此阶段的相对位移.
两个阶段的相对位移之和就是总划痕的长度.
解答:解:设物块刚放上时与传送带的接触点为P,则物块速度小于v=2m/s时,物块受到的摩擦力向下,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma1
解得:a1=10m/s2
物块速度达到2m/s所用的时间为t1,则有:
v=a1t1
解得:t1=0.2s
物块相对传送带向后滑过的距离为:
△L1=vt1-
a1t12
解得:△L1=0.2m
物块的速度达到2m/s后,物块速度大于传送带速度,摩擦力变为向上,由牛顿第二定律得:
mgsinθ-μmgcosθ=ma2
解得:a2=2m/s2
物块此时到离开传送带经历的时间为t2,则有:
L-
a1t12=vt2+
a2t22
解得:t2=1s
此时P点离B点的距离为:
△L2=L-v(t1+t2)
解得:△L2=0.8m
所以传送带上痕迹的长度为:
△L=△L1+△L2=0.2m+0.8m=1m
答:传送带上的划痕长度为1m
mgsinθ+μmgcosθ=ma1
解得:a1=10m/s2
物块速度达到2m/s所用的时间为t1,则有:
v=a1t1
解得:t1=0.2s
物块相对传送带向后滑过的距离为:
△L1=vt1-
| 1 |
| 2 |
解得:△L1=0.2m
物块的速度达到2m/s后,物块速度大于传送带速度,摩擦力变为向上,由牛顿第二定律得:
mgsinθ-μmgcosθ=ma2
解得:a2=2m/s2
物块此时到离开传送带经历的时间为t2,则有:
L-
| 1 |
| 2 |
| 1 |
| 2 |
解得:t2=1s
此时P点离B点的距离为:
△L2=L-v(t1+t2)
解得:△L2=0.8m
所以传送带上痕迹的长度为:
△L=△L1+△L2=0.2m+0.8m=1m
答:传送带上的划痕长度为1m
点评:本题重点是运动分析,要分析透物块的运动,开始是加速,由于重力沿斜面分力大于摩擦力,故物块速度大于传送速度后物块还是加速运动,而不是和传送带一块匀速.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
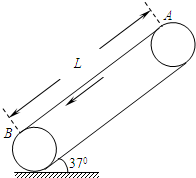 如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转向.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m.小物块在皮带上滑过后会留下痕迹,求小物体离开皮带后,皮带上痕迹的长度.
如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转向.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m.小物块在皮带上滑过后会留下痕迹,求小物体离开皮带后,皮带上痕迹的长度.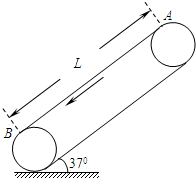 如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转向.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m.小物块在皮带上滑过后会留下痕迹,求小物体离开皮带后,皮带上痕迹的长度.
如图传送带与水平方向夹角37°,在皮带轮带动下,以v0=2m/s的速度沿逆时针方向转向.可视为质点的小物块无初速度放在传送带A点,物块与传送带间的动摩擦因数为0.5,两皮带轮间的距离L=3.2m.小物块在皮带上滑过后会留下痕迹,求小物体离开皮带后,皮带上痕迹的长度.