题目内容
 (2010?奉贤区二模)两个完全相同的物体A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物体受到水平拉力F作用和B物体不受拉力作用的v-t图象,求:
(2010?奉贤区二模)两个完全相同的物体A、B,质量均为m=0.8kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动.图中的两条直线分别表示A物体受到水平拉力F作用和B物体不受拉力作用的v-t图象,求:(1)两物体与地面之间的动摩擦因素μ;
(2)物体A所受拉力F的大小;
(3)12s末物体A、B之间的距离S.
分析:(1)v-t图象的斜率等于加速度,求出B体的加速度,由牛顿第二定律求出动摩擦因数;
(2)由v-t图象求出,A的加速度,由牛顿第二定律列方程,求出物体A所受拉力F的大小;
(3)6s末B物体静止,由图象的“面积”求出12s末A、B两物体的位移,再求解A、B之间的距离s.
(2)由v-t图象求出,A的加速度,由牛顿第二定律列方程,求出物体A所受拉力F的大小;
(3)6s末B物体静止,由图象的“面积”求出12s末A、B两物体的位移,再求解A、B之间的距离s.
解答:解:(1)由v-t图得:aB=
=
m/s2=-
m/s2,
由牛顿第二定律得:-μmg=maB,解得:μ=
=0.067;
(2)由图象得:aA=
=
m/s2=
m/s2,
由牛顿第二定律得:F-f=ma1,解得:F=0.8N;
(3)设A、B在12s内的位移分别为S1、S2,
由v-t图得S1=
×(4+8)×12m=72m,
S2=
×6×4m=12m,
12s末A、B两物体间的距离S=S1-S2=72m-12m=60m;
答:(1)两物体与地面之间的动摩擦因素为0.067;
(2)物体A所受拉力F的大小为0.8N;
(3)12s末物体A、B之间的距离为60m.
| △v2 |
| △t2 |
| 0-4 |
| 6-0 |
| 2 |
| 3 |
由牛顿第二定律得:-μmg=maB,解得:μ=
| 1 |
| 15 |
(2)由图象得:aA=
| △v1 |
| △t1 |
| 8-4 |
| 12-0 |
| 1 |
| 3 |
由牛顿第二定律得:F-f=ma1,解得:F=0.8N;
(3)设A、B在12s内的位移分别为S1、S2,
由v-t图得S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
12s末A、B两物体间的距离S=S1-S2=72m-12m=60m;
答:(1)两物体与地面之间的动摩擦因素为0.067;
(2)物体A所受拉力F的大小为0.8N;
(3)12s末物体A、B之间的距离为60m.
点评:本题首先要根据斜率求出加速度、“面积”求出位移,其次抓住两物体的滑动摩擦力相同.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 (2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( )
(2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( )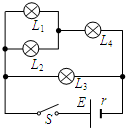 (2010?奉贤区二模)如图所示,电源电动势为E,内阻为r,合上开关S后各电灯都能发光.如果某一时刻电灯L1的灯丝烧断,之后各灯虽亮度变化,但并未损坏,则之后( )
(2010?奉贤区二模)如图所示,电源电动势为E,内阻为r,合上开关S后各电灯都能发光.如果某一时刻电灯L1的灯丝烧断,之后各灯虽亮度变化,但并未损坏,则之后( )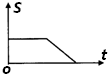 (2010?奉贤区二模)如图是某运动物体的s-t图象,则它的运动情况是.( )
(2010?奉贤区二模)如图是某运动物体的s-t图象,则它的运动情况是.( )