题目内容
(20分)如图所示,两根相距L=1.0m的光滑平行金属导轨水平固定放置,导轨距水平地面H=0.8m,导轨的左端通过电键连接一电动势E=4.0V、内阻r=1.0Ω的电源,在距导轨上横跨一质量为m=0.5kg、有效电阻为R=1.0Ω的金属棒,整个装置处在磁感应强度为B=0.5T方向竖直向上的匀强磁场中。将电键接通后,金属棒在磁场力的作用下沿导轨向右滑动,最终滑离导轨.
求:(1)金属棒在滑动过程中的最大加速度及离开导轨后有可能达到的最大水平射程;
(2)若金属棒离开导轨后的实际水平射程仅为0.8m,则从闭合电键到金属棒离开导轨在金属棒上产生的焦耳热为多少?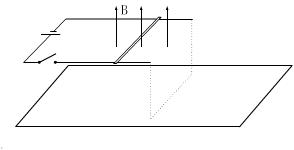
(1)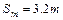
(2)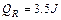
解析(1)在电键刚闭合时,回路中电流最大,金属棒加速度最大。设此时回路中电流为I,金属棒所受安培力为F,则有: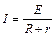 ……………………………………(3分)
……………………………………(3分)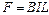 ……………………………………(1分)
……………………………………(1分)
根据牛顿第二定律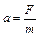 ………………………………………(1分)
………………………………………(1分)
代入数值后得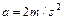 ………………(1分)
………………(1分)
电键闭合后,金属棒在导轨上做加速度逐渐减小的加速运动,若金属棒离导轨右端较远,则金属棒有可能在达到最大速度后离开导轨平抛,这种情况下水平射程最大。设金属棒能达到的最大速度为vm,从抛出到落地所用时间为t,则: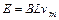 ………………………………………(2分)
………………………………………(2分)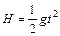 ………………………………………(1分)
………………………………………(1分) …………………………………………(1分)
…………………………………………(1分)
代入数值后解得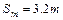 …………………(1分)
…………………(1分)
(2)若金属棒实际射程为S=0.8m,则金属棒离开导轨时的速度为 ……………………………………………………(1分)
……………………………………………………(1分)
设金属棒在导轨上运动时间为Δt ,此过程回路中平均电流为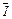 ,通过电量为
,通过电量为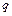 ,则:
,则: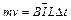 ………………………………………………(3分)
………………………………………………(3分)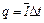 ……………………………………………………(1分)
……………………………………………………(1分)
根据能量守恒,回路中产生热量为Q,则: ……………………………………………………(2分)
……………………………………………………(2分)
根据串联电路特点,金属棒上产生的热量为: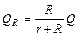 ……………………………………………………(1分)
……………………………………………………(1分)
代入数值后可解得: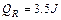 …………………(1分)
…………………(1分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案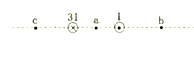
| A、a点和b点的磁感应强度方向相同 | B、a点和b点的磁感应强度大小之比为8:1 | C、c点和b点的磁感应强度方向相同 | D、c点和b点的磁感应强度大小之比为5:1 |
 如图所示,两根相距L平行放置的光滑导电轨道,与水平面的夹角均为 α,轨道间有电阻R,处于磁感应强度为B、方向竖直向上的匀强磁场中,一根质量为m、电阻为r的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计.求:
如图所示,两根相距L平行放置的光滑导电轨道,与水平面的夹角均为 α,轨道间有电阻R,处于磁感应强度为B、方向竖直向上的匀强磁场中,一根质量为m、电阻为r的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计.求: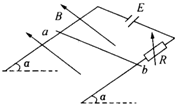 如图所示,两根相距l=0.25m平行放置的导电轨道,倾角α=30°,B=0.8T的匀强磁场垂直轨道平面向上.今在导轨上放一重为2N,电阻不计的金属杆ab,其最大静摩擦力为金属棒对导轨压力的
如图所示,两根相距l=0.25m平行放置的导电轨道,倾角α=30°,B=0.8T的匀强磁场垂直轨道平面向上.今在导轨上放一重为2N,电阻不计的金属杆ab,其最大静摩擦力为金属棒对导轨压力的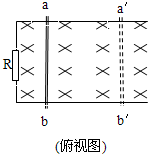 如图所示,两根相距L=0.5m,处于同一水平面平行金属直导轨,放置在磁感应强度B=2.0T、方向竖直向下的匀强磁场中,导轨左端用导线边接一个定值电阻R,一根垂直导轨的金属棒在△t=0.5s时间内,由位置ab匀速滑动到位置a′b′,使闭合电路的磁通量由1.5Wb增大到2.5Wb.
如图所示,两根相距L=0.5m,处于同一水平面平行金属直导轨,放置在磁感应强度B=2.0T、方向竖直向下的匀强磁场中,导轨左端用导线边接一个定值电阻R,一根垂直导轨的金属棒在△t=0.5s时间内,由位置ab匀速滑动到位置a′b′,使闭合电路的磁通量由1.5Wb增大到2.5Wb.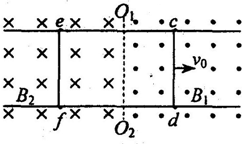 如图所示,两根相距L=0.5m的平行金属足够长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,分界线O1O2右侧为磁感应强度B1=0.6T方向竖直向上的匀强磁场,左侧为磁感应强度为B2=0.4T方向竖直向下的匀强磁场,导轨上横放着两条金属细杆,构成矩形闭合回路,每条金属细杆的质量m=0.2kg,电阻为R=1.5Ω,回路中其余部分电阻可不计.开始时,ef速度为0,给cd一个大小为v0=2.6m/s水平向右的初速度,不计金属细杆与导轨之间的摩擦且接触良好.求:
如图所示,两根相距L=0.5m的平行金属足够长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,分界线O1O2右侧为磁感应强度B1=0.6T方向竖直向上的匀强磁场,左侧为磁感应强度为B2=0.4T方向竖直向下的匀强磁场,导轨上横放着两条金属细杆,构成矩形闭合回路,每条金属细杆的质量m=0.2kg,电阻为R=1.5Ω,回路中其余部分电阻可不计.开始时,ef速度为0,给cd一个大小为v0=2.6m/s水平向右的初速度,不计金属细杆与导轨之间的摩擦且接触良好.求: