题目内容
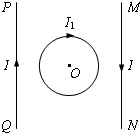 MN和PQ为两条相互平行的长直导线,通有大小相等的电流,电流方向如图所示,两条导线之间有一通电圆环,圆环与导线位于同一平面内,圆环中心O点到两条导线的距离相等,已知O点的磁感应强度为B,通电圆环在O点产生的磁感强度为B1,则两通电直导线在O点产生的磁感应强度为
MN和PQ为两条相互平行的长直导线,通有大小相等的电流,电流方向如图所示,两条导线之间有一通电圆环,圆环与导线位于同一平面内,圆环中心O点到两条导线的距离相等,已知O点的磁感应强度为B,通电圆环在O点产生的磁感强度为B1,则两通电直导线在O点产生的磁感应强度为B-B1
B-B1
,若取走直导线MN,则O点的磁感应强度为| B+B1 |
| 2 |
| B+B1 |
| 2 |
分析:根据通电导线周围存在磁场,由右手螺旋定则来确定磁场的方向,再由矢量叠加原理,则可确定通电直导线在O点的磁感应强度.
解答:解:根据右手螺旋定则可知,直导线PQ、MN及环导线在O点的磁场方向均相同,且它们在O点的合磁感应强度为B,而通电圆环在O点产生的磁感强度为B1,因此由矢量叠加原则可知,两通电直导线在O点产生的磁感应强度为B-B1;
若取走直导线MN,由于两直导线的电流大小相等,所以O点的磁感应强度为B1+
=
.
故答案为:B-B1、
若取走直导线MN,由于两直导线的电流大小相等,所以O点的磁感应强度为B1+
| B-B1 |
| 2 |
| B+B1 |
| 2 |
故答案为:B-B1、
| B+B1 |
| 2 |
点评:考查右手螺旋定则、矢量叠加原理:方向相同则相加,方向相反则相减.

练习册系列答案
相关题目
 (其它电阻不计),与滑轨间的动摩擦因数均
(其它电阻不计),与滑轨间的动摩擦因数均 =0.5,先固定cd棒,问:
=0.5,先固定cd棒,问: =10m/s的速度做匀速直线运动?
=10m/s的速度做匀速直线运动? 
 (其它电阻不计),与滑轨间的动摩擦因数均
(其它电阻不计),与滑轨间的动摩擦因数均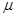 =0.5,先固定cd棒,问:
=0.5,先固定cd棒,问: =10m/s的速度做匀速直线运动?
=10m/s的速度做匀速直线运动? 

