Question

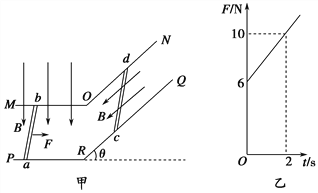
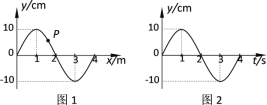
【题目】如图1所示，竖直边界分别为P和Q的区域宽度为4L，其内部分布着垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场，电场随时间变化的关系如图2所示，E>0表示电场方向竖直向上．在t＝0时刻，一带电量为＋q、质量为m的带电微粒从边界P上的A点处水平射入该区域，先沿直线运动到某点，再经历一次完整的半径为L的匀速圆周运动，最后沿直线运动从边界Q上的B点处离开磁场，重力加速度为g.求：

(1) 图2中的E0；

(2) 微粒刚进入磁场时的速度v0及磁场的磁感应强度B；

(3) 电场变化周期T的范围。

Answer 1

【答案】(1) (2) ； (3) (1＋π)≤T≤(＋π)

【解析】

(1) 由带电微粒做匀速圆周运动可得

qE0＝mg

得

E0＝

(2) 由带电微粒做直线运动可知

Bqv0＝mg＋qE0

由带电微粒做匀速圆周运动可得

Bqv0＝m

由上述两式解得

v0＝

B＝

(3) (Ⅰ) 如图1所示，当O点为AB中点时，所对应的周期T为最小周期

微粒从A运动至O点处所需要的时间为t1

t1＝＝＝

微粒做匀速圆周运动的周期为t2

t2＝＝π

则最小周期

Tmin＝t1＋t2＝(1＋π)

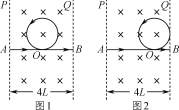
(Ⅱ) 如图2所示，当圆轨道与右边界Q相切时，所对应的周期T为最大周期

微粒从A运动至O点处所需要的时间为t1

t1＝＝＝

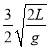
微粒做匀速圆周运动的周期为t2

t2＝＝

则最大周期

Tmax＝t1＋t2＝(＋π)

综上所述，电场变化周期T的范围是(1＋π)≤T≤(＋π)