题目内容
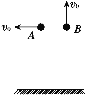
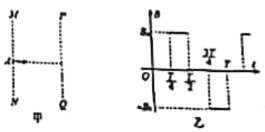
【题目】如图甲所示,在平行虚线MN、PQ间有垂直于纸面的交变磁场,两虚线间的距离为d,磁场的磁感应强度随时间变化的规律如图乙,磁场变化的周期为T.一质量为m、电荷量为q的带电粒子在虚线MN上的A点以垂直于MN向右射入两虚线间,若磁场的磁感应强度![]() ,不计粒子的重力,则下列说法正确的是
,不计粒子的重力,则下列说法正确的是
A. 粒子在磁场中做圆周运动的周期也为T
B. 粒子在t=T/8时刻射入,粒子会从虚线MN射出
C. 要使粒子在两虚线间能做一个完整的圆周运动,粒子的速度最大可以为![]()
D. 要使粒子在两虚线间能做两个完整的周运动,粒子的速度最大可以为![]()
【答案】CD
【解析】
根据牛顿第二定律,由洛伦兹力提供向心力,结合圆周运动的周期公式,可求出周期;分析各个时间段内粒子的运动情况,判断粒子是否会从MN虚线射出;粒子在两个虚线间做一个完整的圆周运动,最大半径等于d/2,再由半径公式求出最大速度;根据几何关系分析粒子在两个虚线间做两个完整圆周运动的条件,再结合半径公式即可求出速度。
粒子在磁场中做圆周运动的周期![]() ,故A错误;粒子在t=T/8时刻射入,在T/8~T/4 之间粒子会沿直线向右运动,在T/4~T/2时间内做一个完整的圆周运动回到虚线上,在T/2~3T/4时间粒子又沿直线向右运动,不会从虚线MN射出,故B错误;要使粒子在两虚线间能做一个完整的圆周运动,粒子的最大半径为r=d/2,根据
,故A错误;粒子在t=T/8时刻射入,在T/8~T/4 之间粒子会沿直线向右运动,在T/4~T/2时间内做一个完整的圆周运动回到虚线上,在T/2~3T/4时间粒子又沿直线向右运动,不会从虚线MN射出,故B错误;要使粒子在两虚线间能做一个完整的圆周运动,粒子的最大半径为r=d/2,根据![]() 得,粒子的最大速度为
得,粒子的最大速度为![]() ,故C正确;要使粒子在两虚线间能做两个完整的圆周运动,则粒子在两虚线间的运动满足v0
,故C正确;要使粒子在两虚线间能做两个完整的圆周运动,则粒子在两虚线间的运动满足v0![]() +2r=d,得
+2r=d,得![]() ,故D正确;故选CD。
,故D正确;故选CD。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目