题目内容
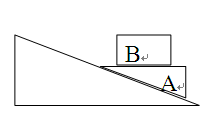
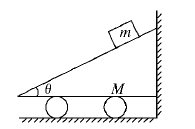
如图所示，质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上，P、Q之间的动摩擦因数为μ1，Q与斜面间的动摩擦因数为μ2(μ1>μ2)．当它们从静止开始沿斜面滑下时，两物体始终保持相对静止，则物体P受到的摩擦力大小为多少？
μ2mgcosθ
先取PQ为一整体，受力分析如图所示．
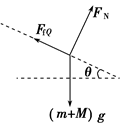
由牛顿第二定律得：
(M＋m)gsinθ－FfQ＝(M＋m)a
FfQ＝μ2FN
FN＝(m＋M)gcosθ
以上三式联立可得a＝gsinθ－μ2gcosθ
再隔离P物体，设P受到的静摩擦力为FfP，
方向沿斜面向上，对P再应用牛顿第二定律得：
mgsinθ－FfP＝ma
可得出FfP＝μ2mgcosθ.
由牛顿第二定律得：
(M＋m)gsinθ－FfQ＝(M＋m)a
FfQ＝μ2FN
FN＝(m＋M)gcosθ
以上三式联立可得a＝gsinθ－μ2gcosθ
再隔离P物体，设P受到的静摩擦力为FfP，
方向沿斜面向上，对P再应用牛顿第二定律得：
mgsinθ－FfP＝ma
可得出FfP＝μ2mgcosθ.
练习册系列答案
名校课堂系列答案
相关题目
