题目内容
19. 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线栓在竖直挡板上,球与挡板间有一根被压缩的轻质弹簧,当烧断细线时,小球被弹出,小球离开平台前弹簧已恢复原长,已知小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线栓在竖直挡板上,球与挡板间有一根被压缩的轻质弹簧,当烧断细线时,小球被弹出,小球离开平台前弹簧已恢复原长,已知小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10m/s2)( )| A. | 25J | B. | 20J | C. | 15J | D. | 10J |
分析 小球离开平台做平抛运动,平抛运动在竖直方向上做自由落体运动,根据h=$\frac{1}{2}$gt2求出小球空中运动的时间.求出小球在竖直方向上的分速度,从而得知水平分速度.
解答 解:由h=$\frac{1}{2}$gt2得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.5}{10}}=\sqrt{\frac{3}{10}}s$
则落地时竖直方向上的分速度vy=gt=10×$\sqrt{\frac{3}{10}}$m/s.
tan60°=$\frac{{v}_{y}}{{v}_{0}}$,解得v0=$\sqrt{10}$m/s.
所以弹簧被压缩时具有的弹性势能为物体所获得动能,即为$\frac{1}{2}m{{v}_{0}}^{2}=10J$,故D正确,ABC错误;
故选:D
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.平抛运动的时间由高度决定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 一物体静止在光滑的水平桌面上,现对其施加水平力,使它沿水平桌面做直线运动,该物体的速度-时间图象如图所示.根据图象判断下列说法中正确的是( )
一物体静止在光滑的水平桌面上,现对其施加水平力,使它沿水平桌面做直线运动,该物体的速度-时间图象如图所示.根据图象判断下列说法中正确的是( )
 一物体静止在光滑的水平桌面上,现对其施加水平力,使它沿水平桌面做直线运动,该物体的速度-时间图象如图所示.根据图象判断下列说法中正确的是( )
一物体静止在光滑的水平桌面上,现对其施加水平力,使它沿水平桌面做直线运动,该物体的速度-时间图象如图所示.根据图象判断下列说法中正确的是( )| A. | 0s~2s时间内物体的位移为零 | |
| B. | 2s末和6s末物体距离出发点的距离相等 | |
| C. | 0s~1s时间内与3s~4s时间平均速度相同 | |
| D. | 0s~1s时间内与2s~3s时间内水平力对物体所做的功相等 |
14. 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )| A. | 运动周期相同 | B. | 运动线速度一样 | C. | 向心力相同 | D. | 向心加速度相同 |
4.纸带上已按要求选出0,1,2,3,4,5,6七个计数点,相邻计数点间的距离一次为x1、x2、x3、x4、x5、x6,则可以判断和计算出( )
| A. | 计数点0对应速度v0一定为0 | |
| B. | 根据v1=$\frac{{x}_{1}+{x}_{2}}{2T}$可计算一号点的对应速度,同理可算出v2,v3,v4,v5 | |
| C. | 无法计算出v0和v6的大小 | |
| D. | 可作出v-t图象求出斜率即加速度 |
11.一质量为m的物体在空中加速下落,加速下落的加速度大小为a,且a<g(g为重力加速度),在物体下落h高度的过程中,下列说法中正确的是( )
| A. | 重力势能减小了mah | B. | 动能增大了mah | ||
| C. | 动能增大了m(g-a)h | D. | 机械能损失了m(g-a)h |


 如图所示.在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨.导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一报金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.己知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.求:
如图所示.在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨.导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一报金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.己知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.求: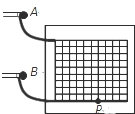 如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则:B球进入水平轨道后将做匀速直线运动;实验中只要A球能落到下面的轨道上,总能观察到A球正好砸在B球上,由此现象可以得出的结论是A球在水平方向做匀速直线运动.
如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则:B球进入水平轨道后将做匀速直线运动;实验中只要A球能落到下面的轨道上,总能观察到A球正好砸在B球上,由此现象可以得出的结论是A球在水平方向做匀速直线运动.