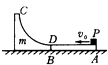
题目内容
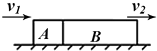
【题目】如图，甲乙两光滑小球原在水平面以相同速度向右运动，现甲向右运动要通过一段坡路ABC，乙要经过一个坑DEF，若经ABC和DEF的路程相等，两球通过C或F到达右端水平面时速度相等，则
A. 甲由A到C的时间比乙由D到F的短
B. 甲由A到C的时间比乙由D到F的长
C. 甲从A到C的过程中加速度先较小再增大
D. 乙从D到F的过程中加速度先增大再减小再增大再减小
【答案】BD
【解析】试题分析：根据两小球的速度变化判断运动时间；将小球的运动看作在倾斜角在变化的斜面上的运动，结合牛顿第二定律分析解题．
设两球在A、D两点的速度为v，甲先减速后加速，整个过程中的平均速度小于v，而乙先加速后减速，整个过程中的平均速度大于v，而ABC和DEF的路程相同，所以根据
可知乙球所用时间段，甲球所用时间长，A错误B正确；甲的运动过程中，从A到B过程中，坡与水平方向的夹角从0到0，设为
， 
先增大后减小，从B到C过程，坡度也是从0到0，故
先增大后减小，而根据牛顿第二定律可得运动的加速度为
，故从A到C过程中，加速度先增大后减小，再增大再减小，乙的运动过程中，也是如此，坡度先增大后减小，再增大在减小，故乙的加速度先增大再减小再增大再减小，C错误D正确．
练习册系列答案
相关题目
