题目内容
如图所示,M是一块平面镜,位于透明液体中,镜面水平向上放置,镜面到液面的距离h=0.8m。一束细光线竖直向下射来,通过液体射到平面镜上。现将平面镜以入射点为水平轴顺时针转过18.5°角,转到图中虚线所示的位置,光线经平面镜反射后,在液面处分成两束,且这两束光恰好垂直,求镜面旋转后光从开始进入液面到第一次离开液面的时间。(设平面镜较短,光线在平面镜上只发生一次反射,sin37°=0.6)
8×10-9s
解析试题分析:将平面镜绕水平轴转过15°角,反射光线将转过30°,反射光线在液面处的入射角等于30°,而反射光在液面处形成的反射光与折射光垂直,画出光路图,根据几何知识求出入射角为i=30°,折射角为r=60°,算出折射率n,结合公式 可求出光在液体中的传播速度,再找出光在液体中通过的路程,可求出时间。
可求出光在液体中的传播速度,再找出光在液体中通过的路程,可求出时间。
依题意作出光路图如图所示当镜面转过18.5°角时,反射光线转过37°角,
即∠AOO′=∠OO′N′=37°,由几何知识可得∠CO′N=53° (1分)
则液体的折射率 ①(2分)
①(2分)
光在液体中的路程为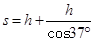 ②(1分)
②(1分)
光在液体中的速度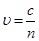 ③(2分)
③(2分)
光从开始进入液面到第一次离开液面的时间 ④(1分)
④(1分)
由①~④式并代入数据可得t=8×10-9s (2分)
考点:折射率的两种求法,光路作图

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示,当氢原子从n=4迁到n=2的能级和从n=3迁到n=1的能级时,分别辐射出光子a和光子b,则
| A.由于放出光子,原子的能量增加 |
| B.光子a的能量小于光子b的能量 |
| C.光子a的波长小于光子b的波长 |
| D.若光子a能使某金属发生光电效应,则光子b不一定能使该金属发生光电效应 |
用一束紫外线照射某金属时没有产生光电效应,下列措施中可能产生光电效应的是
| A.换用强度更大的紫外线照射 | B.换用红外线照射 |
| C.延长紫外线照射时间 | D.换用极限波长较大的金属 |
(4分)下列说法正确的是 .
| A.汤姆生发现了电子,并提出了原子的栆糕模型 |
| B.太阳辐射的能量主要来自太阳内部的热核反应 |
| C.一束光照射到某种金属上不能发生光电效应,是因为该束光的强度小 |
| D.将放射性元素掺杂到其它稳定元素中,并降低其温度,该元素的半衰期将增大 |


 和n2=
和n2= ,求:
,求:

