题目内容
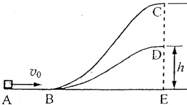 如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,c点的高度为2h.一滑块从A点以初速度v0分别的沿两轨道滑行到C或D处后水平抛出.求
如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,c点的高度为2h.一滑块从A点以初速度v0分别的沿两轨道滑行到C或D处后水平抛出.求(1)滑块从C处落到水平面的时间;
(2)滑块从C处落到水平面时,落点与E的距离;
(3)为实现落点与E的距离SCE<SDE,v0应满足什么条件?
分析:(1)平抛运动在竖直方向上做自由落体运动,根据高度求出运动的时间.
(2)平抛运动在水平方向上做匀速直线运动,根据动能定理求出物块运动到C处的速度,结合速度和平抛运动的时间求出落地点与E的距离.
(3)求得sC和sD的大小的表达式,根据题意分析可以得出,v0应满足的条件.
(2)平抛运动在水平方向上做匀速直线运动,根据动能定理求出物块运动到C处的速度,结合速度和平抛运动的时间求出落地点与E的距离.
(3)求得sC和sD的大小的表达式,根据题意分析可以得出,v0应满足的条件.
解答:解:(1)根据2h=
gt2,解得t=
.
(2)根据动能定理得,-mg?2h=
mv2-
mv02
解得v=
.
则sc=vt=
.
(3)同理sD=
.
因为sc=
.
要SCE<SDE,也就是要有2(v02-4gh)<v02-2gh,
所以v02<6gh,
又滑块必须能到达C点,
即 vC2=v02-4gh,
所以 v02>4gh,
因此初速度应满足
<υ0<
.
答:(1)滑块从C处落到水平面的时间t=
(2)滑块从C处落到水平面时,落点与E的距离Sc=
(3)v0应满足
<υ0<
.
| 1 |
| 2 |
|
(2)根据动能定理得,-mg?2h=
| 1 |
| 2 |
| 1 |
| 2 |
解得v=
| v02-4gh |
则sc=vt=
|
|
(3)同理sD=
|
|
因为sc=
|
|
要SCE<SDE,也就是要有2(v02-4gh)<v02-2gh,
所以v02<6gh,
又滑块必须能到达C点,
即 vC2=v02-4gh,
所以 v02>4gh,
因此初速度应满足
| 4gh |
| 6gh |
答:(1)滑块从C处落到水平面的时间t=
|
(2)滑块从C处落到水平面时,落点与E的距离Sc=
|
|
(3)v0应满足
| 4gh |
| 6gh |
点评:整个过程中,物体的机械能守恒,离开C和D后物体做平抛运动,根据平抛运动的规律分析可以得出结论.

练习册系列答案
相关题目
 (2010?上海)如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出.
(2010?上海)如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出. 如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出。
如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出。 分别沿两轨道滑行到C或D处后水平抛出。
分别沿两轨道滑行到C或D处后水平抛出。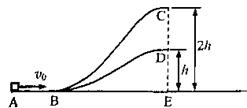
 和
和 .
.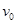 分别沿两轨道滑行到C或D处后水平抛出。
分别沿两轨道滑行到C或D处后水平抛出。
 和
和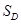 .
.