题目内容
在波的传播方向上有两个质点P和Q,它们的平衡位置相距s="1.2" m,且大于一个波长,介质中的波速为v="2" m/s,P和Q的振动图线如图12-3-6所示,求振动周期的最大值,并画出t=0时的波的图象.
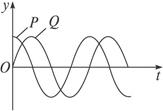
图12-3-6

图12-3-6
(1)波由P点向Q点传播:周期T=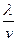 =
=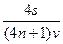 =
=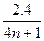 (n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s. t=0时波的图象如图12-3-7所示.
(n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s. t=0时波的图象如图12-3-7所示.
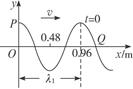
图12-3-7
(2)波由Q点向P点传播:T=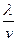 =
=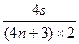 =
=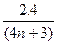 (n=1,2,3,…),当n=1时,λ和T取最大值,其最大值分别为λ2=
(n=1,2,3,…),当n=1时,λ和T取最大值,其最大值分别为λ2=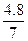 m≈0.69 m,T2=
m≈0.69 m,T2=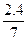 s≈0.34 s,t=0时波的图象如图12-3-8所示.
s≈0.34 s,t=0时波的图象如图12-3-8所示.
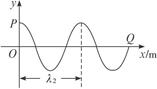
图12-3-8
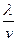 =
=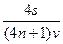 =
=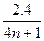 (n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s. t=0时波的图象如图12-3-7所示.
(n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s. t=0时波的图象如图12-3-7所示.
图12-3-7
(2)波由Q点向P点传播:T=
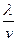 =
=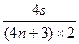 =
=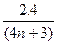 (n=1,2,3,…),当n=1时,λ和T取最大值,其最大值分别为λ2=
(n=1,2,3,…),当n=1时,λ和T取最大值,其最大值分别为λ2=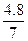 m≈0.69 m,T2=
m≈0.69 m,T2=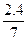 s≈0.34 s,t=0时波的图象如图12-3-8所示.
s≈0.34 s,t=0时波的图象如图12-3-8所示.
图12-3-8
(1)波由P点向Q点传播
由振动图线可知Q点的振动在时间上比P点至少落后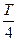 ,因而P、Q两点之间的距离至少是
,因而P、Q两点之间的距离至少是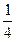 λ,根据波的周期性,s与λ的关系应为(注意题目中s>λ)
λ,根据波的周期性,s与λ的关系应为(注意题目中s>λ)
s=nλ+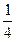 λ(n=1,2,3,…) λ=
λ(n=1,2,3,…) λ=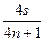 (n=1,2,3,…)
(n=1,2,3,…)
故周期T=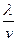 =
=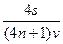 =
=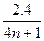 (n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s.
(n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s.
下面作出t=0时波的图象,要正确画出该时刻波的图象,须把握好以下几点:
①根据题中振动图象,t=0时P点位移yP=A,速度vP=0;Q点位移yQ=0,速度最大,且将向正最大位移振动.
②以P点为原点,PQ为x轴画出直角坐标系,并根据s=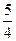 λ1及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出,然后画出经过这两点的一条图象,如图12-3-7所示.
λ1及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出,然后画出经过这两点的一条图象,如图12-3-7所示.
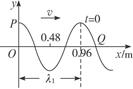
图12-3-7
(2)波由Q点向P点传播
这种情况下与(1)的求解方法基本相同.
所以s=nλ+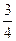 λ(n=1,2,3,…)
λ(n=1,2,3,…)
λ=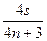
T=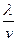 =
=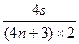 =
=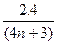 (n=1,2,3,…)
(n=1,2,3,…)
当n=1时,λ和T取最大值,其最大值分别为λ2=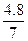 m≈0.69 m,T2=
m≈0.69 m,T2=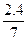 s≈0.34 s,t=0时波的图象如图12-3-8所示.
s≈0.34 s,t=0时波的图象如图12-3-8所示.
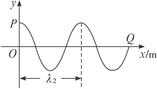
图12-3-8
由振动图线可知Q点的振动在时间上比P点至少落后
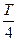 ,因而P、Q两点之间的距离至少是
,因而P、Q两点之间的距离至少是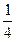 λ,根据波的周期性,s与λ的关系应为(注意题目中s>λ)
λ,根据波的周期性,s与λ的关系应为(注意题目中s>λ)s=nλ+
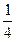 λ(n=1,2,3,…) λ=
λ(n=1,2,3,…) λ=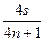 (n=1,2,3,…)
(n=1,2,3,…)故周期T=
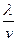 =
=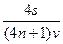 =
=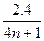 (n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s.
(n=1,2,3,…),显然,n=1时,λ和T有最大值,其最大值分别为λ1="0.96" m,T1="0.48" s.下面作出t=0时波的图象,要正确画出该时刻波的图象,须把握好以下几点:
①根据题中振动图象,t=0时P点位移yP=A,速度vP=0;Q点位移yQ=0,速度最大,且将向正最大位移振动.
②以P点为原点,PQ为x轴画出直角坐标系,并根据s=
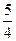 λ1及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出,然后画出经过这两点的一条图象,如图12-3-7所示.
λ1及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出,然后画出经过这两点的一条图象,如图12-3-7所示.
图12-3-7
(2)波由Q点向P点传播
这种情况下与(1)的求解方法基本相同.
所以s=nλ+
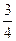 λ(n=1,2,3,…)
λ(n=1,2,3,…)λ=
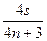
T=
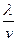 =
=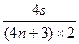 =
=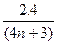 (n=1,2,3,…)
(n=1,2,3,…)当n=1时,λ和T取最大值,其最大值分别为λ2=
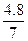 m≈0.69 m,T2=
m≈0.69 m,T2=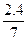 s≈0.34 s,t=0时波的图象如图12-3-8所示.
s≈0.34 s,t=0时波的图象如图12-3-8所示.
图12-3-8

练习册系列答案
相关题目
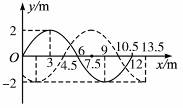
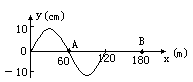
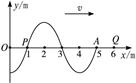
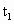 =0时波形如图,波的传播方向向右,已知在
=0时波形如图,波的传播方向向右,已知在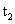 =0.9s时刻A点出现第三次波峰,求:
=0.9s时刻A点出现第三次波峰,求: