题目内容
【题目】如图，在竖直平面内有一固定光滑轨道，其中AB是长为R的水平直轨道，BCD是圆心为O、半径为R的3/4圆弧轨道，两轨道相切于B点。在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力。已知小球刚好能沿圆轨道经过最高点C，重力加速度为g。求：
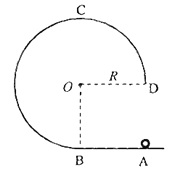
（1）小球在AB段运动的加速度的大小；
（2）小球从D点运动到A点所用的时间。
【答案】（1）
（2）
【解析】（1）小球在BCD段运动时，受到重力mg、轨道压力N的作用，如图所示
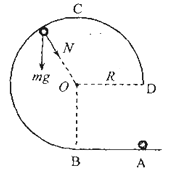
据题意，
，且小球在最高点C所受轨道的正压力为零。
设小球在C点的速度大小为
，根据牛顿第二定律有，
小球从B点运动到C点，根据机械能守恒定律，
设B点处小球的速度大小为
，有
由于小球在AB段由静止开始做匀加速运动，设加速度大小为a，由运动学公式，有
，
建立解得AB段运动的加速度大小a=
（2）设小球在D点处的速度大小为
，下落到A点时的速度大小为V，
由机械能守恒定律有：
设小球从D点运动到A点所用的时间为t，由运动学公式得，
联立解得
练习册系列答案
相关题目
