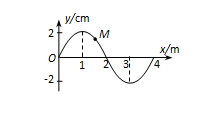题目内容
一列沿x轴传播的横波如图所示,波长λ="8" m,实线表示t1=0时刻的波形图,虚线表示t2="0.005" s时刻的波形图.求:

(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
(3)若t2-t1>T,并且波速为3600 m/s,则波沿哪个方向传播?

(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
(3)若t2-t1>T,并且波速为3600 m/s,则波沿哪个方向传播?
(1)v=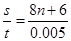 1600n+1200(m/s),(n=0.1.2……,)
1600n+1200(m/s),(n=0.1.2……,)
(2)若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)波是沿x轴向右传播的
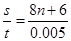 1600n+1200(m/s),(n=0.1.2……,)
1600n+1200(m/s),(n=0.1.2……,)(2)若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)波是沿x轴向右传播的
(1)因为题中没有给出波的传播方向,故需要对波沿x轴正方向和x轴负方向传播分别进行讨论.又因为题中没有给出Δt=t2-t1与周期T的关系,故需要考虑到波的重复性.
若波沿x轴正方向传播,则可看出是波形传播的最小距离s0=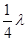 ="2" m
="2" m
波传播的可能距离是s=s0+nλ=8n+2(m)
则可能的波速为v=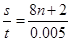 =1600n+400(m/s),(n=0.1.2.,)
=1600n+400(m/s),(n=0.1.2.,)
若波沿x轴负方向传播,则可看出是波形传播的最小距离s0= ="6" m
="6" m
波传播的可能距离是s=s0+nλ=8n+6(m)
则可能的波速为v=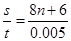 1600n+1200(m/s),(n=0.1.2……,)
1600n+1200(m/s),(n=0.1.2……,)
(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>s>λ,这时波速的通解表达式中n=1.
若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)当t2-t1>T,波速为3600 m/s时,根据波动与振动的相应性可知t2-t1>T,所以波向前传播的距离大于波长s>λ,而且可以计算出
s=vt=3600×0.005=18(m)
由于波长等于8 m,这样波向前传播了 个波长.由波形图不难判断出波是沿x轴向右传播的
个波长.由波形图不难判断出波是沿x轴向右传播的
若波沿x轴正方向传播,则可看出是波形传播的最小距离s0=
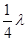 ="2" m
="2" m波传播的可能距离是s=s0+nλ=8n+2(m)
则可能的波速为v=
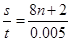 =1600n+400(m/s),(n=0.1.2.,)
=1600n+400(m/s),(n=0.1.2.,)若波沿x轴负方向传播,则可看出是波形传播的最小距离s0=
 ="6" m
="6" m波传播的可能距离是s=s0+nλ=8n+6(m)
则可能的波速为v=
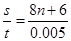 1600n+1200(m/s),(n=0.1.2……,)
1600n+1200(m/s),(n=0.1.2……,)(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>s>λ,这时波速的通解表达式中n=1.
若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)当t2-t1>T,波速为3600 m/s时,根据波动与振动的相应性可知t2-t1>T,所以波向前传播的距离大于波长s>λ,而且可以计算出
s=vt=3600×0.005=18(m)
由于波长等于8 m,这样波向前传播了
 个波长.由波形图不难判断出波是沿x轴向右传播的
个波长.由波形图不难判断出波是沿x轴向右传播的
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
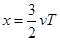 处的质点P,下列说法正确的是 ( )
处的质点P,下列说法正确的是 ( )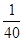 s时
s时