题目内容
 某汽车司机看到交通岗的绿灯亮后,立即以3m/s2的加速度开始起动汽车,去追赶前方330m远、同方向行驶的自行车.设汽车能达到的最大速度为30m/s,自行车以6m/s的速度做匀速直线运动.试求:
某汽车司机看到交通岗的绿灯亮后,立即以3m/s2的加速度开始起动汽车,去追赶前方330m远、同方向行驶的自行车.设汽车能达到的最大速度为30m/s,自行车以6m/s的速度做匀速直线运动.试求:(1)汽车在追上自行车前运动多长时间与自行车相距最远?此时他们之间的距离是多少?
(2)汽车至少要用多长时间才能分追上自行车?
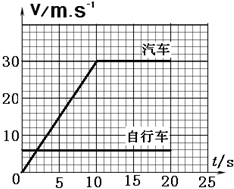
(3)试在如图的坐标中,作出此过程汽车和自行车的速度-时间图象.
分析:(1)由题,汽车做匀加速运动,自行车做匀速直线运动,汽车的速度先小于自行车的速度,后大于自行车的速度,两车的距离先增大后减小,当两车速度相等相距最远,由速度公式求出速度相等所经历的时间,由位移公式求出相距最大的距离;
(2)由速度公式求出汽车速度达到最大值所用的时间,当汽车的位移与自行车的位移之差等于330m时,汽车追上自行车.由位移求出时间.
(2)由速度公式求出汽车速度达到最大值所用的时间,当汽车的位移与自行车的位移之差等于330m时,汽车追上自行车.由位移求出时间.
解答:解:(1)当汽车的速度v1与自行车的速度v2大小相等时,二者相距最远
即v2=at1
所以t1=
=
s=2s
二者之间的距离为△x=v2t1-
a
+x0=(6×2-
×3×22+330)m=336m
(2)汽车达到最大速度所用的时间t2=
=
s=10s
设汽车经时间t能追上自行车,根据路程关系可得
解得t=20s
(3)此过程汽车和自行车的速度-时间图如下图所示.
答:(1)汽车在追上自行车前运动2s与自行车相距最远.此时他们之间的距离是336m.
(2)汽车至少要用20s才能分追上自行车.
(3)此过程汽车和自行车的速度-时间图象如上图所示.
即v2=at1
所以t1=
| v1 |
| a |
| 6 |
| 3 |
二者之间的距离为△x=v2t1-
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
(2)汽车达到最大速度所用的时间t2=
| vm |
| a |
| 30 |
| 3 |
设汽车经时间t能追上自行车,根据路程关系可得
|
解得t=20s
(3)此过程汽车和自行车的速度-时间图如下图所示.

答:(1)汽车在追上自行车前运动2s与自行车相距最远.此时他们之间的距离是336m.
(2)汽车至少要用20s才能分追上自行车.
(3)此过程汽车和自行车的速度-时间图象如上图所示.
点评:本题是追及问题,在分别研究两车各自运动的基础上,关键要抓住两车之间的关系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目