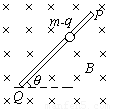题目内容
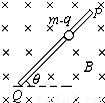
PQ为一根足够长的绝缘细直杆,处于竖直的平面内,与水平夹角为q斜放,空间充满磁感应强度B的匀强磁场,方向水平如图所示。一个质量为m,带有负电荷的小球套在PQ杆上,小球可沿杆滑动,球与杆之间的摩擦系数为m(m<tgq),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中:

(1)小球最大加速度为多少?此时小球的速度是多少?
(2)下滑过程中,小球可达到的最大速度为多大?
【答案】
(1) 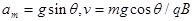 (2)
(2) 
【解析】(1)根据题意因为 ,所以小球刚开始做加速下落,小球下落过程中,竖直向下的重力
,所以小球刚开始做加速下落,小球下落过程中,竖直向下的重力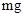 ,垂直斜面向上的洛伦兹力
,垂直斜面向上的洛伦兹力 ,和斜面给的摩擦力
,和斜面给的摩擦力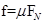 ,刚开始小球的速度比较小,此时
,刚开始小球的速度比较小,此时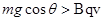 ,即
,即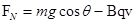 ,小球做加速运动,随着速度的增大,F在增大,
,小球做加速运动,随着速度的增大,F在增大,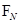 在减小,所以
在减小,所以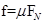 在减小,小球的合力即沿斜面方向的合力
在减小,小球的合力即沿斜面方向的合力 在增大,即小球的加速度在增大,当
在增大,即小球的加速度在增大,当 时小球在垂直斜面方向上的合力为零,即小球与斜面间的正压力为零
时小球在垂直斜面方向上的合力为零,即小球与斜面间的正压力为零 ,所以摩擦力为零,
,所以摩擦力为零, ,之后
,之后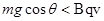 ,
, ,此时小球仍在做加速运动,随着速度的增大,
,此时小球仍在做加速运动,随着速度的增大,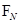 在增大,f在增大,所以
在增大,f在增大,所以 在减小,即加速度在减小,所以当
在减小,即加速度在减小,所以当 时加速度最大,因为此时
时加速度最大,因为此时 ,所以
,所以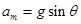 ,
, ,(2)当
,(2)当 时,加速度为零,速度达到最大,最后小球
时,加速度为零,速度达到最大,最后小球 做减速运动,所以
做减速运动,所以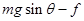 有最大速度,故
有最大速度,故 ,
,
所以
思路分析:小球在向下滑落的过程中,受到的洛伦兹力 是变力,导致小球与斜面间的正压力
是变力,导致小球与斜面间的正压力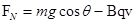 在变化,从而导致小球的合力
在变化,从而导致小球的合力 在变化,可通过分析
在变化,可通过分析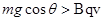 ,
, ,
,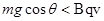 三个过程中小球的运动情况,找出加速度最大,速度最大的临界条件,从而解题
三个过程中小球的运动情况,找出加速度最大,速度最大的临界条件,从而解题
试题点评:本题考查了牛顿运动定律与电磁学相结合的题目,是一道小型综合题,关键是找出加速度最大,速度最大的临界条件,突破口是分析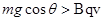 ,
, ,
,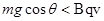 三个过程中小球的运动情况,
三个过程中小球的运动情况,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 PQ为一根足够长的绝缘细直杆,处于竖直的平面内,与水平夹角为θ斜放,空间充满磁感应强度B的匀强磁场,方向水平如图所示.一个质量为m,带有负电荷的小球套在PQ杆上,小球可沿杆滑动,球与杆之间的摩擦系数为μ(μ<tgθ),小球带电量为q.现将小球由静止开始释放,试求小球在沿杆下滑过程中:
PQ为一根足够长的绝缘细直杆,处于竖直的平面内,与水平夹角为θ斜放,空间充满磁感应强度B的匀强磁场,方向水平如图所示.一个质量为m,带有负电荷的小球套在PQ杆上,小球可沿杆滑动,球与杆之间的摩擦系数为μ(μ<tgθ),小球带电量为q.现将小球由静止开始释放,试求小球在沿杆下滑过程中: (
( ),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中:
),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中: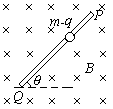
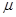 (
(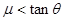 ),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中:
),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中: