题目内容
 如图所示,用半径为0.4m的电动滚轮在长薄铁板的上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10.0kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板南静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5.0rad/s,g=10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板的上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10.0kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板南静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5.0rad/s,g=10m/s2.求:
(1)铁板和滚轮分离时铁板的速度;
(2)加工一块这样的铁板电动机要消耗多少电能?(不考虑电动机自身的能耗)
分析:(1)刚开始砂轮对铁板有滑动摩擦力,则可根据f=μN求出滑动摩擦力大小,再由此公式求出工作台对铁板的摩擦阻力,从而由牛顿第二定律来求出铁板的加速度;根据s=
可求出铁板达到砂轮的速度时的位移,与铁板的长度比较,确定分离的速度..
(2)根据功能关系和能量守恒定律可知,消耗的总电能等于系统增加的动能和内能之和,故可先求出铁板动能增量,再由Q=f△s求出产生的热能,从而得到消耗的电能.
| v2 |
| 2a |
(2)根据功能关系和能量守恒定律可知,消耗的总电能等于系统增加的动能和内能之和,故可先求出铁板动能增量,再由Q=f△s求出产生的热能,从而得到消耗的电能.
解答:解:(1)开始砂轮给铁板向前的滑动摩擦力 F1=μ1FlN=0.3×100N=30N;
工作台给平板的摩擦阻力 F2=μ2F2N=0.1×(100+l0×10)N=20N<F1;
因而铁板先向右做匀加速直线运动a=
=1m/s2;
加速过程铁板达到的最大速度 vm=ωR=5×0.4m/s=2m/s;
这一过程铁板的位移s1=
=2m,刚好等于铁板的长度,此时正好分离;
故铁板先以1m/s2的加速度做匀加速直线运动,当速度达到最大时,刚好分离.
(2)根据功能关系和能量守恒定律可知,消耗的总电能等于系统增加的动能和内能之和;
铁板动能增量为,△Ek=
mv2=
×10×22J=20J;
铁板与滚轮间的相对路程为,△S=vmt1-s1=2×2-2=2m;
铁板与滚轮间因摩擦产生的热量为Q1=F1△S=30×2J=60J;
铁板与地面间因摩擦产生的热量为Q2=F2L=20×2.8J=56J;
因而消耗的电能为E=△Ek+Q1+Q2=136J;
故消耗的电能为136J.
答:(1)铁板和滚轮分离时铁板的速度2m/s;
(2)加工一块这样的铁板电动机要消耗136J的电能.
工作台给平板的摩擦阻力 F2=μ2F2N=0.1×(100+l0×10)N=20N<F1;
因而铁板先向右做匀加速直线运动a=
| F1-F2 |
| m |
加速过程铁板达到的最大速度 vm=ωR=5×0.4m/s=2m/s;
这一过程铁板的位移s1=
| ||
| 2a |
故铁板先以1m/s2的加速度做匀加速直线运动,当速度达到最大时,刚好分离.
(2)根据功能关系和能量守恒定律可知,消耗的总电能等于系统增加的动能和内能之和;
铁板动能增量为,△Ek=
| 1 |
| 2 |
| 1 |
| 2 |
铁板与滚轮间的相对路程为,△S=vmt1-s1=2×2-2=2m;
铁板与滚轮间因摩擦产生的热量为Q1=F1△S=30×2J=60J;
铁板与地面间因摩擦产生的热量为Q2=F2L=20×2.8J=56J;
因而消耗的电能为E=△Ek+Q1+Q2=136J;
故消耗的电能为136J.
答:(1)铁板和滚轮分离时铁板的速度2m/s;
(2)加工一块这样的铁板电动机要消耗136J的电能.
点评:本题中铁板的运动有加速过程和匀速过程,容易忽略加速过程,消耗的电能可由功能关系和能量守恒定律相结合求解!

练习册系列答案
相关题目
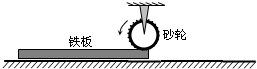 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.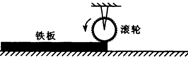 如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10kg.已知滚轮与铁板间的动摩擦因数为0.5,忽略铁板与工作台面间的摩擦.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.0m、质量为10kg.已知滚轮与铁板间的动摩擦因数为0.5,忽略铁板与工作台面间的摩擦.铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.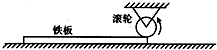 如图所示,用半径为0.4m的电动滚轮在薄铁板上表面压轧一道浅槽,铁板长L=2.8m,质量m=10Kg,已知滚轮与铁板,铁板与工作台面间的动摩擦因数分别为0.3和0.1,开始时把铁板的右端放入滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦力作用下铁板由静止开始向右运动并被压轧出一浅槽,已知滚轮转动的角速度恒为5rad/s,g取10m/s2,求:
如图所示,用半径为0.4m的电动滚轮在薄铁板上表面压轧一道浅槽,铁板长L=2.8m,质量m=10Kg,已知滚轮与铁板,铁板与工作台面间的动摩擦因数分别为0.3和0.1,开始时把铁板的右端放入滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦力作用下铁板由静止开始向右运动并被压轧出一浅槽,已知滚轮转动的角速度恒为5rad/s,g取10m/s2,求: