题目内容
水平冰面的同一直线上有三个木箱A、B、C,质量均为60kg.一质量为30kg的猴子停在A上,与A一起以3m/s的速度向右滑向静止的木箱B、C,在接近B时,以6m/s的水平速度跳上木箱B,接近木箱C时再以6m/s的水平对地速度跳上木箱C,最终与C一起运动,若木箱在运动过程中发生碰撞,则碰撞后不再分开,求木箱A、B、C最终运动的速度.
vC=2m/s,方向向右。
解析试题分析:猴子跳离木箱A过程动量守恒,跳离后木箱速度为vA1,
(M+m)v0=mv+MvA1
解得:vA1=1.5m/s
猴子跳上木箱B后再跳离木箱B,B和猴子组成系统动量守恒
mv=mv+MvB1,解得vB1=0
A木箱将追上B木箱发生正碰,AB组成系统动量守恒,碰后速度为vAB,
MvA1=2MvAB,解得vAB=0.75m/s,方向水平向右,
猴子跳上木箱C过程,动量守恒:mv=(m+M)vC
解得vC=2m/s,方向向右。
考点:动量守恒定律。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
在2010年温哥华冬奥会上,首次参赛的中国女子冰壶队喜获铜牌,如图为中国队员投掷冰壶的镜头.在某次投掷中,冰壶运动一段时间后以0.4 m/s的速度与对方的静止冰壶发生正碰,碰后对方的冰壶以0.3 m/s的速度向前滑行.若两冰壶质量相等,规定向前运动的方向为正方向,则碰后中国队冰壶获得的速度为( ).
| A.0.1 m/s | B.-0.1 m/s | C.0.7 m/s | D.-0.7 m/s |
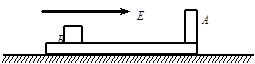
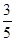 ,碰撞时间极短,则碰撞后滑板速度多大?(均指对地速度)
,碰撞时间极短,则碰撞后滑板速度多大?(均指对地速度)
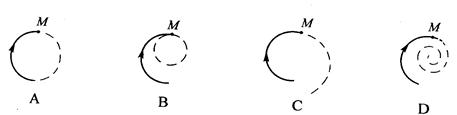
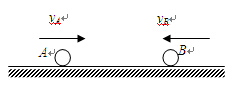
 vB C.vA=
vB C.vA=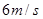 ,B球的速度是
,B球的速度是 ,不久A、B两球发生了对心碰撞。对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现的是( )
,不久A、B两球发生了对心碰撞。对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现的是( )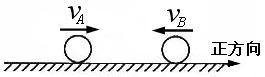
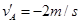 ,
,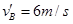 B.
B.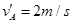 ,
,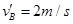
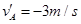 ,
, D.
D. ,
,