题目内容
如图所示，在空间存在这样一个磁场区域，以MN为界，上部分的匀强磁场的磁感应强度为B1，下部分的匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向均垂直纸面如图所示，且磁场区域足够大．在距离界线为h的某点有一带负电荷的A离子与一不带电的粒子B同时以某一速度以平行于界线MN的速度向右运动．粒子A质量为m，带电荷q，经过界线MN时的速度方向与界线成60°角进入下部分磁场．当粒子B沿与界线平行的直线到达位置Q点时（Q点在图中没有标出），恰好又与粒子A第一次相遇．不计A、B粒子的重力．求：（1）P、Q两点间距离．
（2）粒子B运动的速度大小．
分析：（1）画出在磁场中运动轨迹，由几何知识求出轨迹的半径，根据轨迹的对称性，由几何知识求出PQ间的距离．
（2）分析轨迹所对应的圆心角，得到时间与周期的关系，即可求解粒子A从P点到Q点的时间．由运动学的公式求解粒子B运动的速度大小；
（2）分析轨迹所对应的圆心角，得到时间与周期的关系，即可求解粒子A从P点到Q点的时间．由运动学的公式求解粒子B运动的速度大小；
解答：解：（1）粒子A的轨迹如图，粒子A在匀强磁场中做匀速圆周运动，洛仑兹力提供向心力，设粒子A的速度为v0，在MN上方运动半径为R1，运动周期为T1，
根据牛顿第二定律和圆周运动公式有：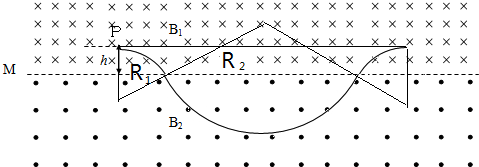
qv0B1=m
，
解得：R1=
=
，
T1=
=
，
同理．粒子A在MN下方运动半径R2和周期T2分别为
R2=
=
=2R1；
T2=
粒子A由P点运动到MN边界时与MN的夹角为60°，则有：
R1-h=R1cos60°
得到：R1=2h，R2=4h．
PQ间的距离为：d=2R2sin60°+2R1sin60°=6
h
（2）粒子A从P点到Q点所用时间为t=
T1+
T2=
+
?
=
则粒子B的从P点到Q点速度为 v=
=
答：（1）P、Q两点间距离为6
h．
（2）粒子B运动的速度大小为
．
根据牛顿第二定律和圆周运动公式有：
qv0B1=m
| ||
| R1 |
解得：R1=
| mv0 |
| qB1 |
| mv0 |
| 2qB1 |
T1=
| 2πR1 |
| v0 |
| πm |
| qB0 |
同理．粒子A在MN下方运动半径R2和周期T2分别为
R2=
| mv0 |
| qB2 |
| mv0 |
| qB0 |
T2=
| 2πm |
| qB0 |
粒子A由P点运动到MN边界时与MN的夹角为60°，则有：
R1-h=R1cos60°
得到：R1=2h，R2=4h．
PQ间的距离为：d=2R2sin60°+2R1sin60°=6
| 3 |
（2）粒子A从P点到Q点所用时间为t=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| πm |
| qB0 |
| 1 |
| 3 |
| 2πm |
| qB0 |
| πm |
| qB0 |
则粒子B的从P点到Q点速度为 v=
| d |
| t |
6
| ||
| πm |
答：（1）P、Q两点间距离为6
| 3 |
（2）粒子B运动的速度大小为
6
| ||
| πm |
点评：本题是有新颖的情景，实质是带电粒子在磁场中运动的类型，画出轨迹，根据轨迹的对称性，由几何知识求出轨迹的半径是解决本题的关键．
练习册系列答案
相关题目
如图所示，在空间存在着水平方向的匀强磁场和竖直方向的匀强电场．电场强度为E，磁感应强度为B．在某点由静止释放一个带电液滴a，它运动到最低点处，恰与一个原来处于静止（悬浮）的液滴b相撞，撞后两液滴合为一体，沿水平方向做直线运动．已知液滴a质量是液滴b质量的2倍，液滴a所带电量是液滴b所带电量的4倍．
（2006?广州模拟）如图所示，在空间存在这样一个磁场区域：以MN为界，上部分的匀强磁场的磁感应强度为B1，下部分的匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向均垂直纸面向里，且磁场区域足够大．在距离界线为h的P点有一带负电荷的离子处于静止状态，某时刻离子分解成为带电粒子A和不带电粒子B，粒子A质量为m、带电荷q，以平行于界线MN的初速度向右运动，经过界线MN时速度方向与界线成60°角，进入下部分磁场．当粒子B沿与界线平行的直线到达位置Q点时，恰好又与粒子A相遇．不计粒子的重力．求：
（2006?黄冈模拟）如图所示，在空间存在着水平向右、场强为E的匀强电场，同时存在着竖直向上、磁感应强度为B的匀强磁场．在这个电、磁场共存的区域内有一足够长的绝缘杆沿水平方向放置，杆上套有一个质量为m、带电荷量为+q的金属环．已知金属环与绝缘杆间的动摩擦因数为μ，且μmg＜qE．现将金属环由静止释放，设在运动过程中金属环所带电荷量不变．
如图所示，在空间存在着水平向右、场强为E的匀强电场，同时存在着竖直向上、磁感强度为B的匀强磁场．在这个电、磁场共同存在的区域内有一足够长的绝缘杆沿水平方向放置，杆上套有一个质量为m、带电荷量为+q的金属环．已知金属环与绝缘杆间的动摩擦因数为μ，且μmg＜qE．现将金属环由静止释放，设在运动过程中金属环所带电荷量不变．