题目内容
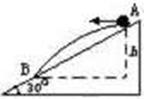
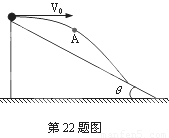
如图所示，一小球从倾角为30°的固定斜面上的A点水平抛出，初动能为6J，则球落到斜面上的B点时动能为（ ）| A、8J | B、10J | C、12J | D、14J |
分析：本题运用运动的分解法研究平抛运动：在水平方向的匀速运动和竖直方向的自由落体运动，又物体落在斜面上，利用好斜面夹角的关系求解即可．
解答：解：设斜面的倾角为α．小球做平抛运动，水平方向做匀速运动，竖直方向做自由落体运动，小球落到斜面上时有：
tanα=
=
=
所以竖直方向速度为vy=gt=2v0tanα
所以速度为v=
=v0
所以小球落到斜面上的速度大小与平抛的初速度的大小成正比．
若α=30°，小球抛出时的动能为6J，则小球落到斜面上时的动能为EK=
mv2=
mv02?（1+4×
）=6×
J=14J
故选：D
tanα=
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
所以竖直方向速度为vy=gt=2v0tanα
所以速度为v=
| v02+vy2 |
| 1+4(tanα)2 |
所以小球落到斜面上的速度大小与平抛的初速度的大小成正比．
若α=30°，小球抛出时的动能为6J，则小球落到斜面上时的动能为EK=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 7 |
| 3 |
故选：D
点评：平抛运动中速度与水平方向，位移与水平方向之间夹角的表达式以及它们之间的关系是经常考查的重点，要加强练习和应用．
练习册系列答案
相关题目
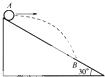
的固定斜面的
点水平抛出，初动能为
，落到斜面上的
点时，其动能是多少？
的固定斜面的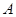
点水平抛出，初动能为
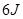，落到斜面上的
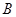点时，其动能是多少？
